Цель работы: ознакомление с явлением интерференции света в тонких прозрачных изотропных средах.
Приборы и принадлежности: микроскоп с осветителем и набором светофильтров, плоскопараллельная пластинка с линзой в оправе, сферометр ИЗС-7.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Если тонкую плёнку осветить монохроматическим светом, то вследствие разделения световой волны на две при отражении и преломлении света на передней и задней поверхностях плёнки возникают две когерентные волны. При сложении двух когерентных волн образуется интерференционная картина, состоящая из чередующихся максимумов и минимумов освещенности. Результат интерференции зависит от оптической разности хода (D), полученной при интерференции двух когерентных волн, идущих в одном направлении.
При наблюдении интерференции в отраженном свете оптическая разность хода равна
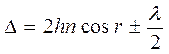
где n – показатель
преломления плёнки, h – толщина пленки, r – угол преломления, 
l/2 – дополнительная разность
хода, возникающая из-за изменения фазы на противоположную при отражении от
плёнки.
Прозрачная пленка может иметь вид клина. Интерференционная картина, получается при отражении света от клина, носит название «полос равной толщины», которые локализованы на поверхности клина.
В работе для получения интерференционной картины используется воздушный клин, образованный между плоскопараллельной пластиной C и плосковыпуклой линзой l (рис. 9.1).
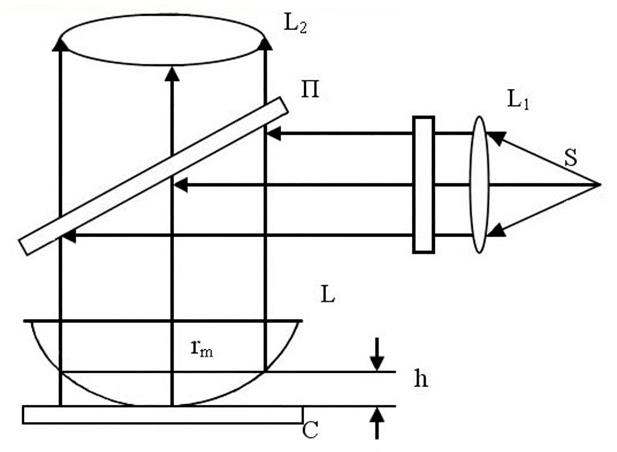
Рис. 9.1.
Интерференционная картина получила название «колец Ньютона». Она состоит из чередующихся светлых и тёмных колец с темным центральным пятном. Для воздушного клина в случае нормального падения монохроматического света разность волн равна
D=2h +(l/2) ;
условия максимума и минимума интенсивности света определяются соответственно выражениями
D=2m (l/2) и D=2(m +1)(l/2) .
Используя приведенные условия, можно получить выражение для радиусов n-го и m-го темных колец Ньютона:
rn=
;
rm= 
.
Тогда радиус кривизны линзы R равен:
.
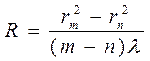Эта формула может служить как для определения радиуса кривизны линзы R, так и для определения длины волны света l.
ОПИСАНИЕ УСТАНОВКИ
Для наблюдения колец Ньютона в работе используется установка, основной частью которой является плосковыпуклая линза с большим радиусом кривизны, положенная на плоскопараллельную пластинку. Интерференционная картина в отраженном свете в виде колец Ньютона наблюдается с помощью микроскопа. Радиус кривизны линзы определяют сферометром ИЗС-7 (рис. 9.2).
Рис. 9.2.
Внутри корпуса 1 сферометра расположен измерительный стержень с миллиметровой шкалой, обеспечивающий контакт сферического наконечника с измеряемым изделием 2. В верхней части корпуса помещается измерительное кольцо 3 с укрепленными на нем тремя шариками. Упор 4 служит для прижатия изделия к измерительному кольцу. Для установки начального отсчета на ноль или на требуемую величину по миллиметровой шкале измерительного микроскопа служит винт 5. Для отвода измерительного стержня вниз служит рычаг-арретир 6. Маховичок 7 окулярного микрометра служит для установки вертикального индекса на нулевое деление круговой шкалы. В установке используется трансформатор 8.
ВЫПОЛНЕНИЕ РАБОТЫ
УПРАЖНЕНИЕ I
Определение радиуса кривизны линзы с помощью
«колец Ньютона» и сферометра
1. Под объектив микроскопа поместить пластинку с линзой в оправе, включить осветитель и, перемещая тубус микроскопа и линзу, сфокусировать микроскоп на четкое видение интерференционной картины («кольца Ньютона»).
2. Используя светофильтр (l=530 нм), провести измерения диаметров темных колец во взаимно перпендикулярных направления dx и dy, начиная с колец более высоких порядков. Цена деления окулярного микрометра 0,02 мм. Найти среднее значение d.
3. Вычислить радиус кривизны линзы по формуле:
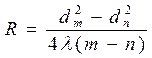, (9.1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.