Физика \ Оптика

Лабораторный практикум по оптике, содержащий описание 21 лабораторной работы, страница 33

Основной частью газового лазера (рис. 11.2) является газоразрядная трубка 1, в которой осуществляется тлеющий газовый разряд. Трубка заполнена смесью неона и изотопа He. Используемый в работе лазер генерирует когерентное излучение с длиной волны
632,8 нм.

В результате взаимодействия атомов неона и гелия с электронами газоразрядной плазмы часть атомов Nе и Не переходят в возбужденное состояние. Атомы гелия, находясь на нестабильных уровнях, могут передавать энергию возбуждения атомам Ne при их столкновениях. Вследствие этого возникает инверсная (обращённая) заселённость возбужденных уровней атомов Ne,что и приводит к процессам вынужденного излучения. Кванты света, распространяющиеся вдоль оси трубки, испытывают многократное отражение от зеркал 2, что обеспечивает большую длину пути в газовой среде, и, следовательно, большую интенсивность излучения. Часть этого излучения проходит через переднее зеркало, коэффициент пропускания которого около 2%.

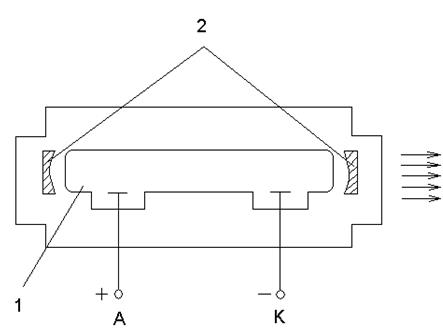
Рис. 11.2.

ВЫПОЛНЕНИЕ РАБОТЫ

УПРАЖНЕНИЕ I

Наблюдение дифракции Фраунгофера на щели

1.  На выходе лазерного луча поместить штатив со щелью. Меняя ширину щели, пронаблюдать зависимость вида дифракционной картины от ширины щели. Зарисовать картину и сделать выводы.

2.  Выбрав ширину щели 0,02 мм, определить положение нескольких минимумов относительно центра картины, удовлетворяющих формуле

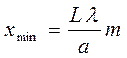 ,                                 (11.3)

где L – расстояние от щели до экрана, a – ширина щели, m – порядок дифракционного минимума.

Формула применима для небольших углов дифракции .

3.  Расстояние между соседними минимумами определить по формуле

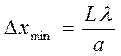                                   (11.4)

Определив координаты минимумов и расстояние между соседними минимумами, оценить ширину щели:

.

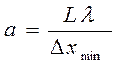Результаты занести в таблицу 1.

Таблица 1.

№ п/п

X(мм)

(мм)

А

(мм)

слева

справа

1

2

3

УПРАЖНЕНИЕ II

Наблюдение дифракции на отверстиях
различной формы

Поместить на выходе лазерного луча поочередно экраны c прямоугольными и круглыми отверстиями, нити различной толщины. Зарисовать наблюдаемые дифракционные картины, сравнить и сделать выводы.

УПРАЖНЕНИЕ III

Дифракция Фраунгофера на одномерной решетке

1.  Поместить на выходе лазерного луча одномерную решетку и определить положения нескольких максимумов относительно центрального (нулевого) максимума.

2.  Определить длину волны излучения газового лазера по формуле

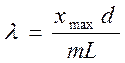 ,                                  (11.5)

где Xmax – координата наблюдаемого максимума относительно центрального, d – постоянная решетки, L – расстояние от решетки до экрана, m – порядок максимума.

Результаты опыта занести в таблицу 2.

Таблица 2.

№ п/п

X(мм)

(мм)

(нм)

(нм)

(нм)

слева

справа

1

2

3

УПРАЖНЕНИЕ IV

Дифракция Фраунгофера на двумерной решетке

1.  Расположить на выходе лазерного луча держатель с набором двумерных дифракционных решеток. Получить дифракционную картину и определить координаты и порядок дифракционных максимумов на экране.

2.  Рассчитать углы дифракции и по расстоянию до экрана L и координатам максимумов (Xmax и Ymax). Из условия главных максимумов определить периоды двумерных решеток.

Результаты занести в таблицу 3.


Таблица 3.

Скачать файл