Прямая линия, проходящая через центры сферических поверхностей, называется главной оптической осью. Пучок световых лучей, распространяющийся параллельно главной оптической оси, после прохождения линзы пересекается в одной точке, называется главным фокусом линзы.
Расстояние от оптического центра линзы до фокуса называют главным фокусным расстоянием линзы. Фокусное расстояние является одной из основных характеристик линзы. Для тонкой линзы теория даёт формулу для нахождения фокусного расстояния линзы:
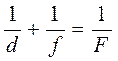(2.1)
где d – расстояние от предмета до оптического центра линзы; f – расстояние от изображения до оптического центра линзы; F – фокусное расстояние линзы.
Величина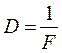 
называется оптической силой линзы.
Оптическая сила измеряется в диоптриях. Одна диоптрия-это оптическая сила такой линзы, у которой фокусное расстояние равно 1м.
Если известны
радиусы кривизны линзы 
и 
и показатель преломления вещества, из
которого она изготовлена, то её фокусное расстояние равно:
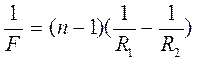(2.2)
В современной оптике отдельные линзы собирают в оптические системы. Системы, у которых оптические центры всех линз расположены на одной прямой, называются центрированными. Простейшей оптической системой называется система, состоящая из двух линз, сложенных вплотную. Для такой системы оптическая сила D равна:
(2.3)
где 
и 
– оптические силы линз, входящих в систему.
Или
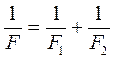(2.4)
Определение фокусных расстояний линз по формуле (2.1) затруднено, так как расстояния d и f отсчитываются от оптического центра линзы, лежащего внутри линзы. Существует ряд косвенных методов определения фокусного расстояния линз и оптических систем.
Одним из наиболее точных методов определения фокусных расстояний является метод Бесселя, заключающийся в следующем: на оптической скамье помещают предмет S и экран, на котором получается изображение S', даваемое линзой или системой линз, расположенной между предметом и экраном (рис. 2.1).
Если расстояние L от предмета до экрана достаточно велико и превышает учетверённое значение фокусного расстояния F , то, перемещая линзу или систему линз вдоль оптической оси, можно найти два таких положения линзы или системы 1 и 2 , при которых на экране наблюдаются чёткое увеличенное и уменьшенное изображения предмета.
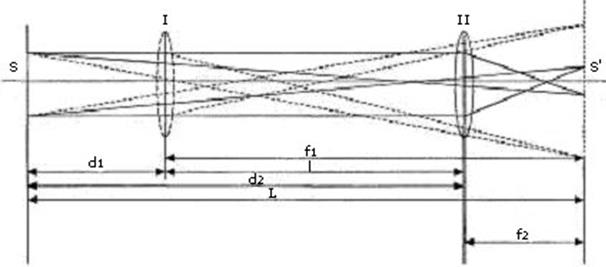
Рис. 2.1.
Обозначим через d1 и f1 расстояние от линзы до предмета и от линзы до изображения при увеличенном изображении предмета и через d2 и f2 те же величины при уменьшенном его изображении. Из рис. 2.1 имеем:
(2.5)
Запишем формулу (2.1) для увеличенного и уменьшенного изображени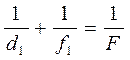й:
и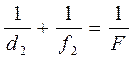 
Откуда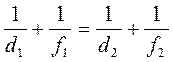 
или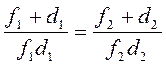 
Так как 
и 
, то
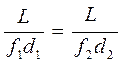(2.6)
Из равенства (2.6) следует, что
(2.7)
Равенства (2.5) и (2.7) одновременно выполняются только при условии, что
и 
(2.8)
Обозначив расстояние между двумя положениями линзы, дающей увеличенное и уменьшенное изображение предмета через l, на основании (2.8) и рис. 2.1 получим:
; 
; 
; 
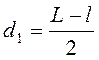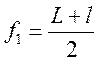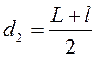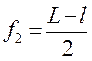(2.9)
Подставляя (2.9) в (2.1) для каждого положения линзы 1 и 2, имеем:
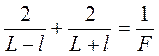(2.10)
Отсюда фокусное расстояние F выразится зависимостью:
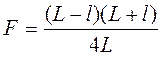(2.11)
В соотношение (2.11) входят только величины L и l , равные расстоянию от предмета до экрана, и расстояния между двумя положениями линзы, легко измеряемые с достаточно большой степенью точности.
ОПИСАНИЕ УСТАНОВКИ
Установка для определения фокусных расстояний линз и оптических систем состоит из двух частей. Одна из них состоит из осветителя с изображаемым предметом (светящейся стрелкой), экрана, рейтера с закреплёнными в ней линзами и предназначена для проведения исследований по методу Бесселя.
Вторая часть состоит из оптического рельса 1 с измерительной линейкой, на котором установлен длиннофокусный коллиматор 2 с мирой 3 или автоколлимационным окуляром со шкалой (рис. 2.2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.