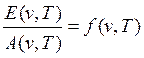 (16.3)
(16.3)
Обозначим для абсолютно
чёрного тела лучеиспускательную способность ![]() , а
поглощательную – a(v,T), тогда
закон Кирхгофа запишется в виде:
, а
поглощательную – a(v,T), тогда
закон Кирхгофа запишется в виде:
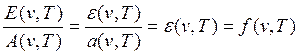 (16.4)
(16.4)
Отсюда видно, что универсальная функция Кирхгофа есть ни что иное, как излучательная способность абсолютно чёрного тела.
Чтобы определить, в какой
области спектра излучает тело, необходимо знать вид функции ![]() . Многочисленные попытки установить вид
функции –
. Многочисленные попытки установить вид
функции – ![]() привели к открытию ряда частных законов
излучения абсолютно чёрного тела.
привели к открытию ряда частных законов
излучения абсолютно чёрного тела.
Первый закон был установлен Стефаном и уточнён в 1884 г. Больцманом. Пользуясь термодинамическим методом, Больцман доказал, что интегральная излучательная способность абсолютно чёрного тела пропорциональна четвёртой степени его абсолютной температуры, т.е.
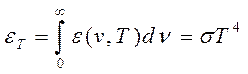 ,
(16.5)
,
(16.5)
где σ – постоянная Стефана-Больцмана.
Закон Стефана-Больцмана касается лишь интенсивности интегрального излучения чёрного тела и ничего не говорит относительно спектрального распределения энергии.
Второй закон,
дающий частотную зависимость функции ![]() , установлен Вином и
имеет вид:
, установлен Вином и
имеет вид:
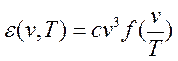 (16.6)
(16.6)
Выражение (16.6) получило название обобщённого закона Вина. От частоты можно перейти к длине волны:
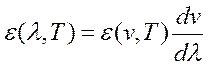 (16.7)
(16.7)
Так как 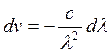 , то
, то
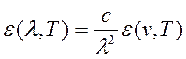 (16.8)
(16.8)
Подставляя (16.8) в (16.6), получим:
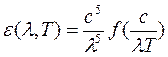
Приравняв нулю
производную ![]() получаем, что положение максимума λmax удовлетворяет условию:
получаем, что положение максимума λmax удовлетворяет условию:
Tλmax=b (16.9)
где b – постоянная, не зависящая от температуры.
В форме записи
(16.9) закон Вина носит название закона смещения Вина. Он показывает, что
положение максимума функции ![]() по мере возрастания
температуры смещается в область коротких волн. Графически это представлено на рис.
16.1.
по мере возрастания
температуры смещается в область коротких волн. Графически это представлено на рис.
16.1.
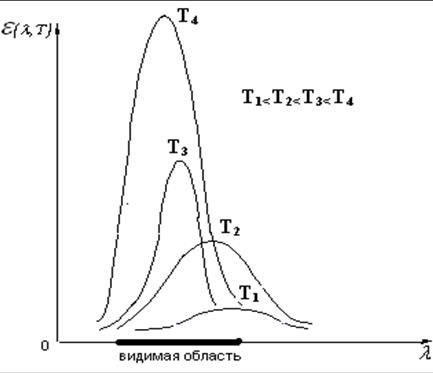
Рис. 16.1.
Из закона Вина следует, что максимальная излучательная способность прямо пропорциональна пятой степени абсолютной температуры:
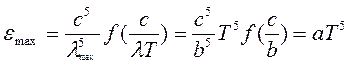 (16.10)
(16.10)
Для установления характера излучения
абсолютно чёрного тела необходимо знать вид функции ![]() .
Частные законы (Больцмана, Вина) не помогли дать общего решения поставленной
задачи. Наиболее приемлемый вид функции был найден Релеем и уточнён Джинсом.
.
Частные законы (Больцмана, Вина) не помогли дать общего решения поставленной
задачи. Наиболее приемлемый вид функции был найден Релеем и уточнён Джинсом.
В обобщенном виде соотношение получило название формулы Релея-Джинса:
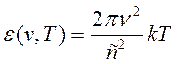 , (16.11)
, (16.11)
где k – постоянная Больцмана.
Однако в области больших частот кривая, полученная по формуле (16.11), сильно отличается от экспериментальной кривой, а интегральная излучательнпая способность обращается в бесконечность (рис. 16.2). Это несоответствие получило название "ультрафиолетовой катастрофы":
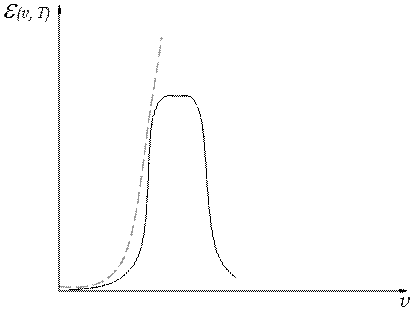
Рис. 16.2.
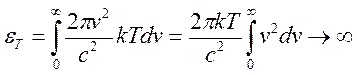
Это означает, что равновесие между телом и его излучением установится только при температуре тела, равной абсолютному нулю.
Причина вышеуказанных трудностей связана с одним из основных положений классической физики, согласно которому энергия системы может изменяться непрерывно.
В 1900г.,
выдвинув новую теорию, согласно которой осциллятор излучает и поглощает свет
дискретно, то есть отдельными порциями (квантами) с энергией ![]() , Планку удалось установить вид функции
, Планку удалось установить вид функции ![]() , хорошо согласующийся с экспериментом:
, хорошо согласующийся с экспериментом:
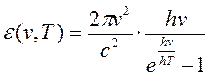 (16.12)
(16.12)
Эта формула получила название формулы Планка. Из формулы Планка следуют все частные законы теплового излучения абсолютно чёрного тела.
Проинтегрируем
выражение (16.12) от 0 до ∞ по v, обозначим
через 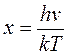 , тогда
, тогда 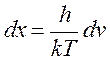 .
Отсюда
.
Отсюда 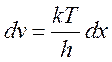 .
.
С учётом обозначений:
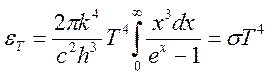 ,
,
где
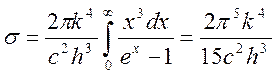 ,
,
т.е. получили закон Стефана-Больцмана. Постоянная Планка отсюда:
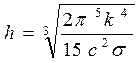 (16.13)
(16.13)
В области малых частот при
условии hv<<kT,
разлагая ![]() в ряд и ограничиваясь первым
членом, получим:
в ряд и ограничиваясь первым
членом, получим:
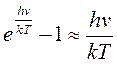 .
.
Тогда формула Планка (16.12) переходит в формулу Релея-Джинса:
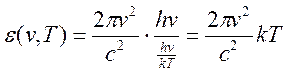
Также можно показать, что из формулы Планка следуют законы Вина. Для этого необходимо, взяв производную от
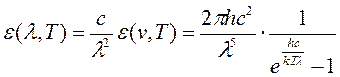
по λ, приравнять её нулю. Результатом будет закон Вина.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.