|
Порядок макси-мума m |
направление x |
направление y |
||||||||
|
Xmax |
L |
|
dx |
|
Y max |
L |
|
dy |
|
|
|
1 |
||||||||||
|
2 |
||||||||||
|
3 |
||||||||||
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Принцип Гюйгенса-Френеля. Зоны Френеля.
2. Дифракция Фраунгофера на щели.
3. Дифракционная решетка и ее свойства. Двумерная решетка. Дифракционная решетка как спектральный прибор.
4. Принцип генерации света в оптических квантовых генераторах.
Цель работы: познакомить студентов с дифракцией Фраунгофера, измерить периоды решеток, изучить последовательность формирования линзой оптического изображения и осуществить пространственную фильтрацию изображения.
Приборы и принадлежности: дифрактометр ИФ-124, микроскоп МБИ-1, дифракционная насадка, репродукционная насадка, одномерные и двумерные объекты, объективный микрометр, щель в круглой оправе.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Явление огибания световой волной соизмеримых с длиной волны препятствий, расположенных на еепути, называют дифракцией света. Различают дифракцию света Френеля и Фраунгофера. Если дифракционная картина образована источником света, лежащем на конечном расстоянии от препятствия, то от него во все стороны распространяется сферическая волна. Дифракцию света в сферических волнах называют дифракцией Френеля. Дифракция света в параллельных лучах, когда источник света находится в бесконечности, называется дифракцией Фраунгофера.
Рассмотрим дифракцию света на пространственной структуре, которая может представлять собой систему неоднородностей, расположенных периодически. В этом случае волна распространяется в среде, в которой имеются участки, где скорость света отличается от скорости в остальных участках среды.
Пусть решетка образована рядом одинаковых рассеивающих центров, расположенных вдоль прямой MМ’ на расстоянии d друг от друга (рис. 12.1).
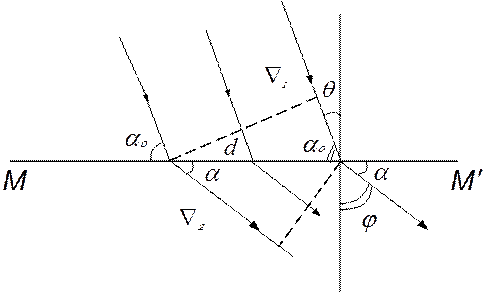
Рис. 12.1.
Такую решетку называют одномерной. Направим на решетку под углом θ пучок параллельных когерентных лучей. Из лучей, рассеиваемых центрами, выберем лучи, которые составляют с нормалью угол φ. Разность хода Δ между соседними лучами равна
Δ=Δ1–Δ2 = d sinθ – d sinφ.
Главные максимумы возникают при условии, что Δ = mλ.
Тогда
d (sinθ — sinφ) = m1λ , (12.1)
где m1 = 0,1,2,3,... .
Для упрощения дальнейшего рассмотрения вопроса введем вместо углов θ и φ дополняющие к ним углы ао и а. Тогда равенство (12.1) примет вид:
d (cos a0 - cos a) = m1λ . (12.2)
Совокупность лучей, параллельных образующей конуса, ось которого совпадает с направлением MМ’, соответствует постоянному значению угла а. Выделим те лучи, которые параллельны одной из образующих конуса и лежат в плоскости чертежа (рис. 12.2).
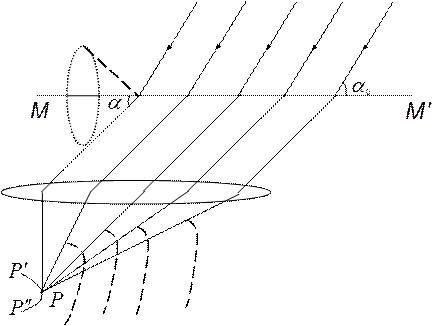
Рис. 12.2.
При выполнении равенства (12.2) эти лучи усилят друг друга, вследствие чего в фокальной плоскости появится светлое пятно Р. Лучи, параллельные другим образующим, дадут свои светлые пятна, и на экране возникнет светлая полоса р’ pp”.
Если a0=
, то значению a=
соответствует светлая полоса
нулевого порядка, которая будет иметь вид прямой. Для нее m1=0. По
обе стороны от нее расположатся гиперболы разных порядков
(рис. 12.3).
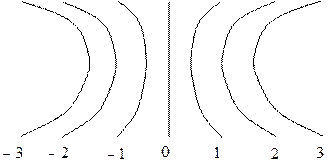
Рис. 12.3.
Для них m1 = ±1, ±2, ... . При большом количестве рассеивающих центров число интерференционных пучков велико, и полосы получаются очень узкими.
Рассмотрим теперь решетку, в которой рассеивающие центры находятся в узлах квадратной решетки, представляющей собой две системы линейных решеток, наложенных друг на друга (рис. 12.4). Пусть, для простоты, периоды решеток одинаковы и равны d.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
