Лабораторный практикум по оптике, содержащий описание 21 лабораторной работы, страница 35

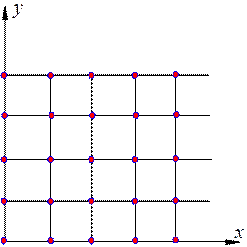
Рис. 12.4.

Тогда максимумы образуются для тех направлений, для которых рассеянные от центров лучи под углами a и b будут удовлетворять условиям

d (cos a₀ -cos a) = m₁λ(12.3)

d (cos β₀ -cos β) =m₂λ

где m₁ , m₂ – целые числа.

Как следует из условия (12.3), в фокальной плоскости линзы для каждого уровня образуется своя система гипербол. Оба условия (12.3) будут выполняться для тех точек, в которых гиперболы пересекаются во взаимно перпендикулярных направлениях (рис. 12.5).

Если на двумерную решетку падает монохроматический свет, дифракционная картина будет иметь вид чередующихся светлых пятен. Если же на решетку падает не монохроматический свет, то каждое пятно растянется в спектр.

В качестве модели дифракционной решетки может служить сетка с очень мелкими ячейками, которая при падении излучения газового лазера дает хорошую дифракционную картину. Если же такую решетку (сетку) осветить рассеянным излучением газового лазера, а после нее поставить линзу, то в фокальной плоскости линзы наблюдается дифракционная картина, а в плоскости наблюдения мы получим изображение сетки.

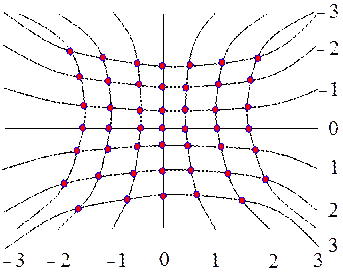
Рис. 12.5.

Фотоснимок математически также может быть описан набором синусоидальных составляющих распределения оптической плотности с различными амплитудами и пространственными частотами. При этом распределение плотности почернений на снимке можно представить набором синусоидальных дифракционных решеток с разной ориентацией, контрастом и периодом.

Если на такой снимок падает сложный световой импульс, то он может быть разложен по теореме Фурье на монохроматические составляющие. Согласно этой теореме любая функция может быть представлена с какой угодно точностью в виде суммы синусоидальных и косинусоидальных функций с соответственно подобранными амплитудами, периодами и начальными фазами.

При этом, если исходная функция периодична (с периодом  Т ), то периоды слагающих синусов и косинусов находятся в простом кратном отношении Т, Т, Т,  Т, …, представленные в виде ряда Фурье. Еслиже функция не периодична, то в разложении находятся не только кратные, но и все возможные периоды, представленные в виде интеграла Фурье. Хорошее приближение получается, если ограничиться даже небольшим числом членов ряда Фурье.

Для этих синусоидальных и косинусоидальных составляющих угол дифракции, определяемый периодом синусоидальных решеток фотоснимка и длиной световой волны, будет различным. По распределению и виду дифракционных максимумов, используя дифрактометр, можно найти распределение периодических структур в исследуемом фотоснимке по пространственным периодам.

Изображение, даваемое линзой, образуется в две стадии:

1) формирование в фокальной плоскости линзы дифракционной картины предмета;

2) преобразование дифракционной картины предмета в фокальной плоскости линзы в изображение предмета в плоскости наблюдения.

Вся информация, имеющаяся в изображении предмета, содержится также и в дифракционной картине предмета. Поэтому, если усилить или ослабить отдельные максимумы, то произойдут соответствующие изменения в изображении предмета. Внесение изменений в дифракционную картину предмета, вызывающих соответствующие изменения в изображении предмета, называется пространственной фильтрацией изображения.

Первым экспериментом, продемонстрировавшим возможность пространственной фильтрации изображения, был опыт Аббе-Портера. В этом опыте металлическая сетка С, образованная проволоками, пересекающимися под прямым утлом, освещалась параллельным пучком света. Сетка размещалась перед линзой Л. В фокальной плоскости линзы на расстоянии F от оптического центра линзы образовывалась дифракционная картина изображения (рис. 12.6).

В плоскости наблюдения на расстоянии f от центра линзы формируется изображение сетки С₁. Если в фокальную плоскость F линзы ввести непрозрачный экран с горизонтально расположенной щелью, то в плоскости наблюдения в изображении сетки будут присутствовать только вертикальные линии.