Электропроводность электролитов. Диффузия в электролитах. Компьютерное моделирование ионной атмосферы, страница 6

Уравнение (II-36) в его общем виде трудно для решения. Чтобы упростить его, примем неавество: еz_ij<< kT, т. е. что электростатическое взаимодействие ионов мало по сравнению с термической энергией. Разложив показательную функцию в ряд

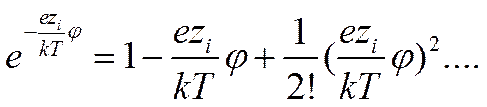                            (I I - 37)

они ограничились  только двумя  его  первыми  членами, получив для ρ следующее уравнение:

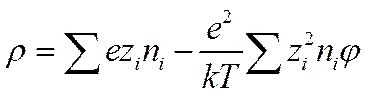                                         (I I-38)

Первый член правой части последнего уравнения  по закону электро­нейтральности равен нулю, откуда

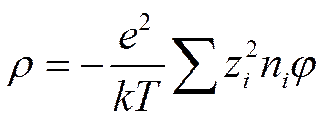
и, следовательно,

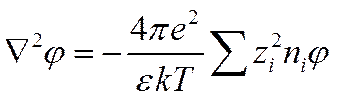                              (I I-39)

или

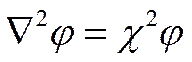                                                   (I I -40)

если ввести обозначение

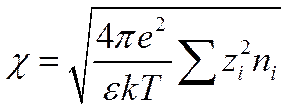                                (I I -41)

Величина χ, точнее 1/ χ, имеет, как это будет показано ниже, большое значение в теории растворов электролитов. Учитывая шаровую симметрию ионной атмосферы, в сферической системе координат вместо Ѳjможно написать:

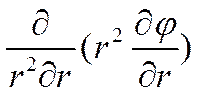                                  (I I-42)

и, подставив это значение Ѳj в уравнение (II-42), получим

                                    (I I-43)

где r— расстояние от центрального иона до места определения потенциала j .

Общее решение этого дифференциального уравнения имеет вид:

                                    (I I-44)

Константы интегрирования A₁и A₂находят из граничных условий. Как следует из основных законов электростатики, при r®¥, j® 0, что является первым граничным условием. Это условие выполняется в том случае, если А₂ = 0, так как иначе с удалением от центрального иона j будет стремиться к бесконеч­ности (е ^χr—величина более высокого порядка, чем r). Следова­тельно, при А₂ = 0

                         (I I -45)

Для определения константы интегрирования A₁в первом при­ближении  предполагается, что ионы можно отождествить с материальными точками, обладающими опре­деленным зарядом. В этом случае при r® 0 потенциал j должен стремиться к потенциалу самого иона j_iт. е.

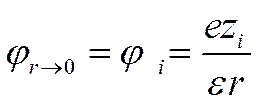                                                            (I I-46)

Если е ^-χr разложить в ряд, то

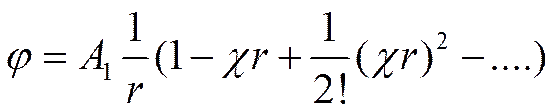
При r® 0 всеми членами ряда можно пренебречь по сравнению с единицей. Тогда

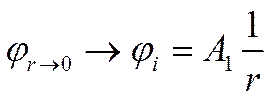
и, следовательно,

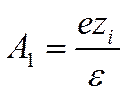                                                         (I I-47)

откуда, а также из (II-45),

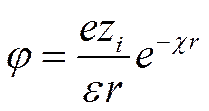                                   (I I-48)

Величина j в уравнении (II-48) представляет собой среднее значе­ние потенциала в точке r, создаваемого ионной атмосферой и цен­тральным ионом. Для реальных растворов специфическим является потенциал ионной атмосферы j_ia, который находят по правилу суперпозиции потенциалов как разность j и j_i

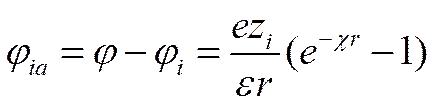
Компьютерное  моделирование ионной атмосферы.

Постановка задачи для моделирования.

В силу сферической симметрии задача является одномерной. В сферической системе координат уравнение Пуассона выглядит следующим образом:

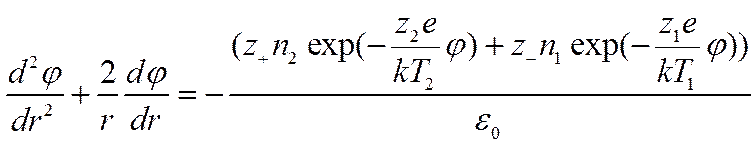
Граничные условия:

r=1e-7м задается потенциал, создаваемый центральным ионом

r=1e-3м задается 0 потенциал (точка считается бесконечно удаленной)

Моделирование осуществлялось в пакете Comsol 3.2. В качестве базового уравнения была выбрана общая форма уравнения Пуассона. Как уже оговаривалось выше задача является одномерной, границы имеют координаты: 1e-7м и 1e-3м.

Сетка сгущается к левому краю модели, параметры построения сетки указаны на рисунке.

Рассматриваемое уравнение в терминах Comsol выглядит следующим образом:

Граничные условия:

Все постоянные задаются в соответсвующем окне:

Для решения уравнения выбран стационарный нелинейный решатель, включена опция сильной нелинейности, количество итераций – 50:

Анализ результатов

Сравним графики потенциала для линейного приближения, экспоненциального и потенциал центрального иона без учета объемного заряда (решение уравнение Лапласа):

Потенциал, создаваемый только центральным ионом существенно отличается от остальных графиков. Рассмотрим более подробно графики вблизи радиуса Дебая: