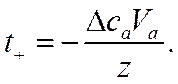
![]()
и
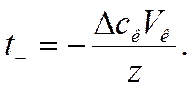
![]()
Так как
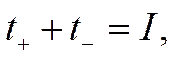
то из выражений (IV-41) и (IV-42) следует, что
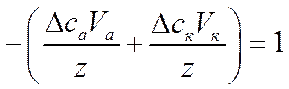
или
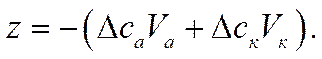
Числа переноса в этой системе можно найти, не применяя кулонометра, а используя опытные данные по изменению концентрации электролита в анодном и катодном пространствах:
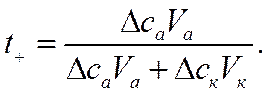
![]()
и
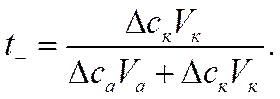
![]()
Подбирая соответствующие электрохимические системы, можно определить числа переноса для любых электролитов.
Метод перемещающейся границы.
Второй метод определения чисел переноса, получивший особенное распространение за последние годы, называется методом перемещающейся границы. Сущность его заключается в том, что задают некоторый ток и через определенный промежуток времени определяют расстояние, пройденное границей между двумя растворами с одним общим ионом. Граница между двумя растворами особенно отчетливо видна в тех случаях, когда один из них окрашен. Если оба раствора бесцветны, но обладают различной плотностью, тогда граница между ними будет видна благодаря различию в показателях преломления. В том и другом случаях наблюдение за перемещением границы проводят при помощи отсчетного микроскопа.
На рис. 9 приведена схема определения по этому методу подвижности ионов кадмия. При включении тока (в направлении, указанном на рис. 9) в растворе появляются ионы кадмия и образуется граница между растворами хлорида кадмия и соляной кислоты, перемещающаяся по мере прохождения тока снизу вверх. Если за некоторое время τ граница пройдет расстояние l, эквивалентное объему V = ΙΩ, где Ω — сечение трубки, то число перенесенных
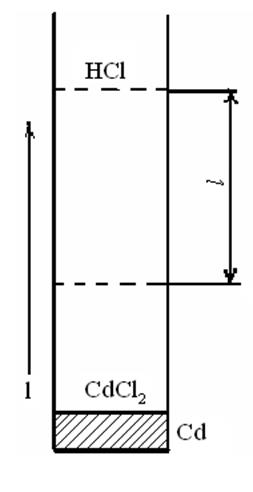
Рис. 9. Схема определения подвижностей ионов по методу перемещающейся границы
грамм-эквивалентов CdCl2 будет равно cV, где с — концентрация CdCl2. При силе тока / общее количество прошедшего электричества составит lτ/Fфарадеев и, следовательно, число переноса иона Cd2+ будет равно
![]()
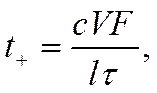
![]()
что отвечает уравнению (IV-38).
Граница между растворами CdCl2 и НС1 видна достаточно отчетливо из-за различной удельной проводимости электролитов. В данном случае χHCl>>χCdCl2 и IR(HCl) <IR(CdCl2) или (Dj/l)HC1 < (Dj/l) CdCl2 , т. е. градиент поля в растворе CdCl2 больше, чем в растворе НС1. Поэтому, если в результате временного перерыва тока более быстрые ионы водорода окажутся в зоне CdCl2, то под действием повышенного градиента поля они опередят более медленные ионы Cd2+ и вновь вернутся в область соляной кислоты. Наоборот, если ионы Cd2+ перейдут в зону соляной кислоты, то их скорость уменьшится в связи с пониженным значением градиента поля. Они отстанут от ионов Н+ и вновь •окажутся в растворе хлорида кадмия. Обычно для большей четкости границы в предварительных опытах подбирают оптимальные концентрации пограничных растворов, обеспечивающие соблюдение так называемого регулирующего соотношения Кольрауша
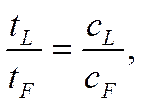
где индексы Fи Lотносятся соответственно к электролитам с быстрыми и медленными ионами, в данном случае к растворам НСl и CdCl2.
Данные, полученные с помощью методов перемещающейся границы и Гитторфа, совпадают друг с другом.
Определение ионных подвижностей.
Опытные данные по электропроводности и числам переноса можно использовать для вычисления ионных подвижностей. Из уравнения (IV-29) следует, что для 1-1 валентного электролита при бесконечном разбавлении, где степень диссоциации α равна единице, эквивалентная проводимость представляет собой сумму ионных подвижностей
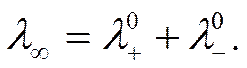
![]()
Вместо уравнений (IV-32) и (IV-33) можно написать
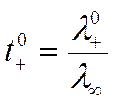 и
и 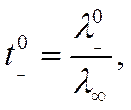
![]()
откуда по известным t0+ и λµлегко найти подвижности ионов при бесконечном разведении.
Уравнение, аналогичное (IV-47), справедливо не только при бесконечном разбавлении, но для бинарных электролитов также и при любой концентрации с. В этом легко убедиться, подставив в (IV-30) и (IV-31) значения соответствующих токов из (IV-23), (IV-24) и (IV-25), тогда
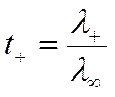 и
и 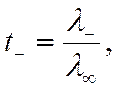
![]()
где λi — подвижность ионов в растворе с концентрацией с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.