Подставляя в (2.5) значение r (х) из уравнения (2.4), получаем уравнение Пуассона — Больцмана (П—Б)
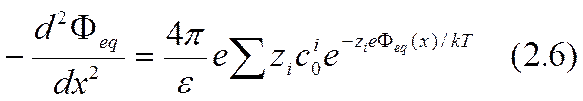
Уравнение (2.6) можно непосредственно проинтегрировать, если, как это было принято Гуи и Чепменом, диэлектрическая постоянная сохраняет постоянное значение на любом расстоянии от поверхности
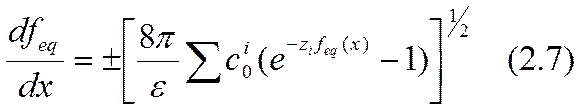
причем учитывается, что на больших расстояниях от поверхности электрическое поле обращается в нуль. Если zifeq<<1 или zi Феq << 25 мВ при комнатной температуре, то степенные функции в правой части уравнения (2.7), можно разложить в ряды и от каждого из них взять только по два первых члена. В результате интегрирования полученного простейшего линейного уравнения имеем
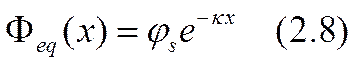
где
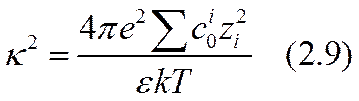
(js — значение потенциала на поверхности). Уравнение (2.8) показывает, что потенциал уменьшается в е раз на расстоянии х-1, а на несколько больших расстояниях убывает практически до нуля. Это обстоятельство позволило характеризовать толщину ДС величиной дебаевского радиуса экранирования х-1. Для водных растворов одновалентных солей
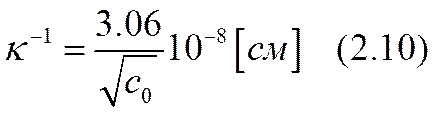
где с0 — молярная концентрация.
В случае симметричного электролита уравнение (2.7) существенно упрощается:
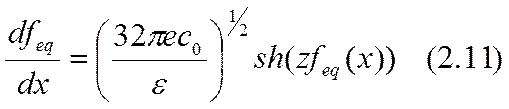
Отсюда можно вывести формулу, связывающую заряд и потенциал поверхности:
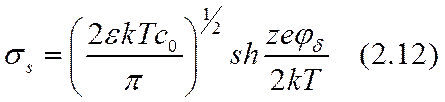
Рассмотренное выше уравнение П—Б для плоской поверхности раздела можно использовать и для описания строения ДС коллоидной частицы, если минимальное значение радиуса кривизны ее поверхности существенно превышает толщину ДС:
![]()
Ионы, непосредственно прилегающие к поверхности, в мощном силовом поле последней не способны к перемещению вдоль нее, поэтому в электрокинетических явлениях принимает участие лишь часть ионов диффузного слоя. Смолуховский (1921 г.) и Фрейндлих ( 1932 г.) предложили различать термодинамические j и z потенциалы, а под электрокинетическим потенциалом понимать лишь часть межфазного скачка потенциала, локализованную в той части ДС, в пределах которой жидкость вовлекается в тангенциальное движение. Фрейндлих предложил назвать эту величину электрокинетическим потенциалом. Он равен потенциалу диффузного слоя в плоскости скольжения, являющейся границей жидкости, вовлекаемой в электроосмотическое скольжение.
Теория Штерна. Строение ДС в рамках теории Гуи определяется только электрическим взаимодействием ионов друг с другом и с поверхностным зарядом, поэтому в теории Гуи фигурирует единственная характеристика ионов - их валентность. Штерн (1924) попытался учесть также роль адсорбционных потенциалов ионов и их размеров.
Специфическую адсорбцию определяют как адсорбцию при электростатическом потенциале, равном нулю. По предположению Штерна, которое в известной мере подтвердилось в дальнейшем, радиус действия сил, обусловливающих специфическую адсорбцию, в отличие от электростатических столь мал, что учет таких сил важен только на расстоянии от поверхности порядка размера ионов. Это дало Штерну основание учитывать влияние адсорбционных сил и конечность размера лишь для ионов, находящихся на минимально возможном расстоянии от поверхности.
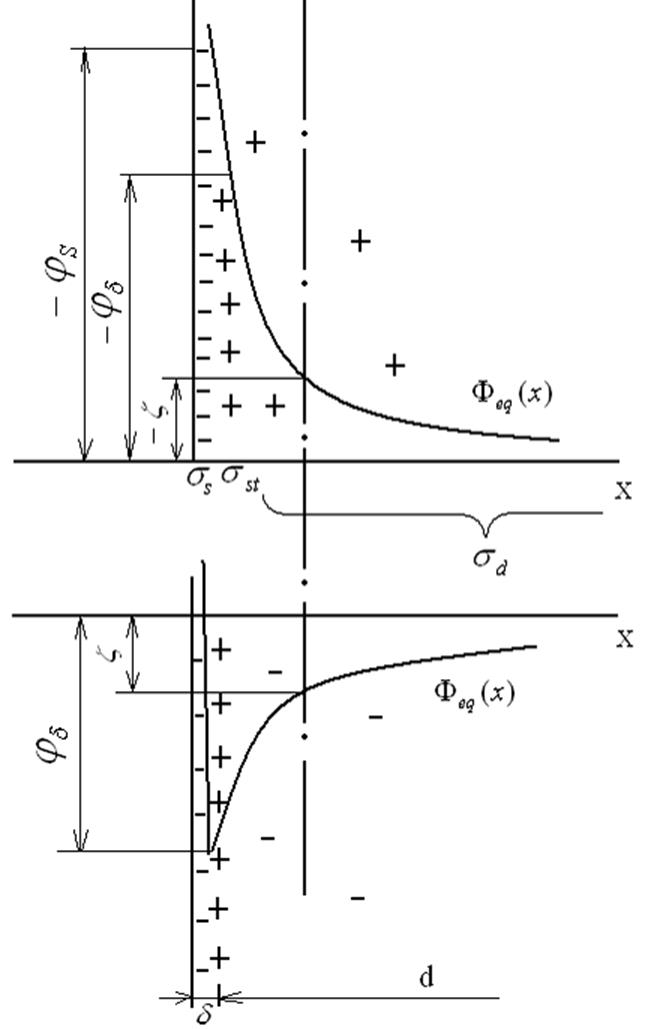
Рис.2.1 Строение ДС по Гуи-Штерну: d – толщина слоя Штерна, d- толщина неподвижной части диффузионного слоя, j0 - потенциал поверхности, jd - потенциал границы слоя Штерна и Гуи, sS - заряд поверхности, sSt - заряд слоя Штерна, sd - заряд слоя Гуи.
Главным в модели Штерна является расчленение ДС на две части — внутреннюю и внешнюю. При этом во внешней части адсорбционные силы и конечный размер ионов игнорируются, что позволяет воспользоваться теорией Гуи. Внутренняя часть — это адсорбционный мономолекулярный слой ионов, который Штерн описывал на базе появившейся незадолго до этого теории мономолекулярной адсорбции на активных центрах (1916 г.), обобщенной Штерном для случая ионов. Поскольку ионы не могут приблизиться к поверхности на расстояние меньше d, Штерн различал максимальное значение потенциала в диффузном слое jd и потенциал стенки js (Введенный Штерном потенциал jd часто называют штерновским.) Поверхностный заряд и монослой адсорбированных противоионов образуют как бы молекулярный конденсатор.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.