причем e равна диэлектрической постоянной среды, заполняющей пространство между обкладками конденсатора.
В растворах, не содержащих поверхностно-активных веществ, емкость ртутного электрода на отрицательной (нисходящей) ветви электрокапиллярной кривой составляет в среднем 20 мкф/см2. Так как
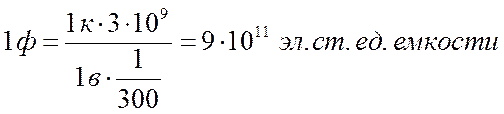
то 1 мкф= 1*10-6 = 9*105 эл. ст. ед. емкости и, следовательно,
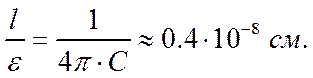
Теория диффузного двойного ионного слоя
В отличие от потенциалопределяющих ионов, для которых характерно сильное специфическое взаимодействие с поверхностью, противоионы даже при сближении с поверхностью обычно находятся под влиянием только электростатических сил. Поскольку противоионы частично сольватированы, расстояние их наибольшего сближения с поверхностью весьма значительно, так что энергия электростатического взаимодействия противоионов с поверхностью не может существенно превышать энергию теплового движения kT. Если энергия ионов в поле притяжения поверхностного заряда порядка kT, тепловое движение должно сделать слой противоионов диффузным. Таким образом, пространственное распределение противоионов определяется тепловым движением и одновременным притяжением к поверхностному заряду, в результате чего образуется диффузная атмосфера определенной притяженности, толщина которой при низких концентрациях электролита может быть весьма значительной.
Поскольку напряженность электрического поля, определяющая силу притяжения противоионов к поверхности, уменьшается с расстоянием от поверхности, для концентрации противоионов также наблюдается аналогичный спад от максимального значения у поверхности, причем у внешней границы избытка концентрации противоионов по сравнению с объемом уже не существует. Ионы, заряженные одноименно с поверхностью и именуемые коионами, или побочными ионами, отталкиваются от поверхности, поэтому их концентрация в пределах ДС ниже, чем в объеме, и убывает с удалением от поверхности. (Закономерность пространственного распределения коионов и противоионов качественно охарактеризована далее на с. 25.)
Количественные закономерности пространственного распределения потенциала Феq (х) и концентраций катионов и анионов C±eq (x) могут быть установлены при учете условий равновесия внутри ДС и законов электростатики. Условием такого равновесия является отсутствие внутри ДС потоков ионов, которое, несмотря на огромные значения напряженности электрического поля в нем, достигается за счет компенсации электромиграционных потоков диффузионными. Противоионы при миграции в электрическом поле должны были бы непрерывно перемещаться к поверхности, но этого не происходит, поскольку концентрация их в этом направлении возрастает и электромиграционный поток полностью компенсируется встречным диффузионным потоком.
Математически условия компенсации электромиграционных и диффузионных потоков представляются в следующем виде (здесь и в дальнейшем с целью сокращения записи два уравнения записываются в виде одного уравнения с двумя индексами. Выбирая верхние индексы, получаем уравнение для катионов, выбирая нижние,— уравнение для анионов):
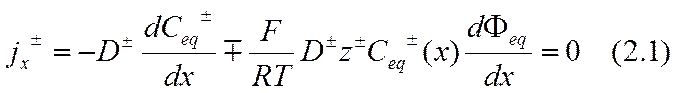
где jx± — суммарные потоки; D±, z± — коэффициенты диффузии и валентность ионов; F — число Фарадея; R — универсальная газовая постоянная; Т — абсолютная температура. Эти два уравнения для трех функций Феq(х) и C±eq (x) позволяют выразить распределения концентрации ионов через распределения потенциала. Интегрирование осуществляется легко, поскольку переменные разделяются:
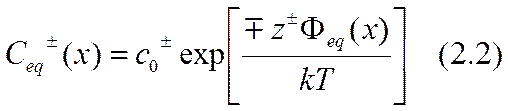
где с0± — значение концентрации ионов в основном объеме электролита, причем здесь учтены граничные условия
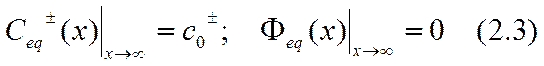
Как и следовало ожидать, ионы распределены по сечению ДС по Больцману, поскольку в двойном слое существует равновесие.
Если заряд типа i равен zie (zi — валентность, положительная для катиона и отрицательная для аниона), то объемная плотность зарядов на расстоянии х от электродов
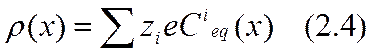
Здесь так же, как и в уравнениях (2.1) и (2.2), принято, что все характеристики ДС являются функциями только расстояния до поверхности. Благодаря этому общее соотношение между электрическим потенциалом Феq (х) и плотностью зарядов в точке х, выражаемой уравнением Пуассона div(eЕ) = 4pr, переходит в одномерную форму:
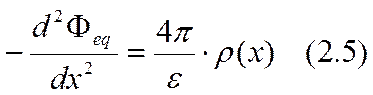
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.