Изучение связи, существующей между направлением и скоростью электрофореза или электроосмоса, с одной стороны, и направлением и напряженностью приложенного электрического поля, с другой, позволяет получить сведения о знаке и величине заряда твердых частиц относительно жидкости и о соответствующем ему скачке потенциала.
Приближенная теория электрокинетических явлений приводит к следующим уравнениям для скорости электроосмоса u и величины потенциала течения (или седиментации) Ε
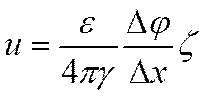
![]()
и
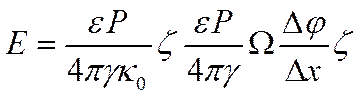
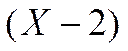
где e — диэлектрическая постоянная жидкой фазы; Δj /Δx— напряженность электрического поля в направлении, параллельном границе раздела твердой и жидкой фаз; γ — вязкость жидкой фазы; k0 —ее удельная электропроводность; Ρ — давление, вызывающее относительное перемещение фаз по границе раздела между ними; Ω — сечение взвешенной частицы (или поры). В случае электрофореза
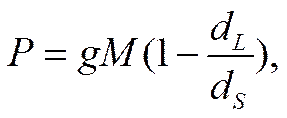
![]()
где g — ускорение силы тяжести; Μ — масса взвешенных частиц, проходящих через 1 см3 сечения микрогетерогенной системы, a dL и ds — плотность жидкости и взвешенных твердых частиц, соответственно.
Величина ζ, входящая в уравнения (Χ-Ι) и (Х-2), называется «дзета-потенциалом» или «электрокинетическим потенциалом»; его можно найти с помощью уравнений (Х-1) и (Х-2), если измерить U или Е. Необходимо, однако, иметь в виду, что уравнения (Х-1) и (Х-2) в силу их приближенности позволяют определить ориентировочные значения ζ-потенциала Непосредственные измерения дают при этом не ζ,, а Dζ/γ, и расчетная величина ζ-потенциала зависит от выбора численных значений D и γ.
В уравнения (Х-1) или (Х-2) подставляют значения диэлектрической постоянной и вязкости жидкой фазы, которые могут не совпадать с диэлектрической постоянной и вязкостью жидкости непосредственно у границы раздела. Рассчитанные по этим уравнениям ζ-потенциалы могут поэтому заметно отличаться от их истинных значений. Помимо того, напряженность поля и удельная электропроводность жидкости вблизи границы раздела т. е. величины, которые следовало бы использовать при расчете ζ-потенциала по уравнениям (Х-1) и (Х-2)] и в глубине жидкой фазы в общем случае не совпадают. Такое различие обусловлено тем, что у поверхности раздела фаз ионный состав обычно иной, чем средний ионный состав всей жидкой фазы.
Первую количественную теорию строения двойного электрического слоя на границе металл — раствор связывают обычно с именем Гельмгольца. По Гельмгольцу (1879), двойной электрический слой можно уподобить плоскому конденсатору, одна из обкладок которого совпадает с плоскостью, проходящей через поверхностные заряды в металле, другая — с плоскостью, соединяющей центры тяжести зарядов ионов, находящихся в растворе, но притянутых
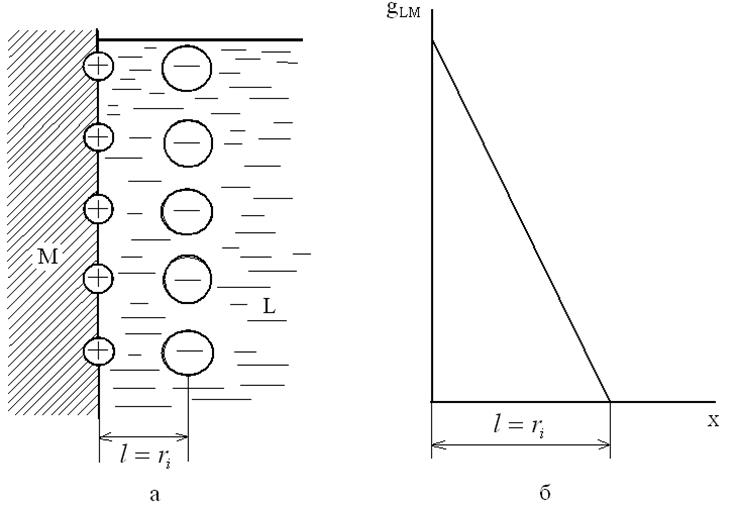
Рис.37. Строение двойного электрического слоя по Геймгольцу: а – молекулярная картина, б – изменение потенциала с расстоянием от границы раздела металл-раствор.
электростатическими силами к поверхности металла (рис. 37). Толщина двойного слоя (т. е. расстояние между обкладками конденсатора) принимается равной радиусу ионов ri. По закону электронейтральности, справедливому и для границы раздела, количество притянутых к поверхности металла ионов должно быть таким, чтобы их заряды как раз компенсировали поверхностные заряды металла, т. е.
![]()
если qм и qL — удельные поверхностные заряды (или плотности заряда) со стороны металла и со стороны раствора.
Из известного уравнения для плоского конденсатора следует, что скачок потенциала между металлом и раствором, обязанный ионному двойному слою, eLM(q) будет прямо пропорционален плотности заряда, т. е.
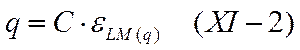
где С — емкость двойного электрического слоя.
Вместе с тем теория конденсированного двойного слоя позволяет получить значения емкостей двойного слоя, согласующиеся с опытом, а при использовании экспериментальных величин емкостей — физически правдоподобную толщину двойного электрического слоя. Для двойного слоя, отвечающего по своим свойствам плоскому конденсатору, можно написать
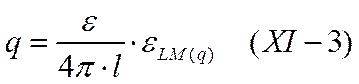
где
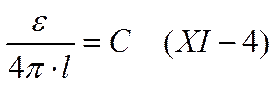
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.