Электропроводность электролитов. Диффузия в электролитах. Компьютерное моделирование ионной атмосферы, страница 17

Заряд поверхности s_s⁺  компенсиро­ван суммой зарядов молекулярного кон­денсатора s_St^-и внешнего диффузионного слоя s_d^-, а полное падение потенциала j_s слагается из падения потенциала в диф­фузной части j_d и разности потенциа­лов между обкладками молекулярного конденсатора (j_s- j_d).

Локализация границы скольжения в рамках рассматриваемой модели до сих пор остается неясной. Некоторые авторы допускали, что эта граница совпадает с границей между слоем Штерна и слоем Гуи и что j_d равно z; однако в общем слу­чае границу можно представить находя­щейся в слое Гуи (рис. 2.1 граница сколь­жения обозначена штрихпунктирной ли­нией). Хотя электрокинетические явле­ния непосредственно связаны с процессами, протекающими в диффузном слое, теория Штерна оказалась весьма полезной при интерпретации экспериментальных данных о зависимости z-потенциала от состава электролита, так как величина этого потенциала чувствительна к изменениям, протекающим в слое Штерна

Поскольку специфическая адсорбция ионов обусловлена силами иного рода, чем силы электростатического притяжения, удерживающие ионы диффузного слоя вблизи поверхности, при добавлении электро­лита в слое Штерна могут выделяться ионы, знак которых совпадает со знаком первоначального заряда поверхности или противоположен ему. Абсолютная величина заряда адсорбированных ионов может ока­заться как меньше, так и больше заряда частицы до введения электро­лита. В частности, противоионы могут адсорбироваться в таком коли­честве, что не только нейтрализуют заряд твердой поверхности, но и перезаряжают ее. В результате характер распределения потенциала в ДС изменится коренным образом (см. рис. 2.1), j_d и z -потенциалы, имевшие ранее тот же знак, что и j_s - потенциал, изменят его на обрат­ный Если для качественной интерпретации электрокинетического потенциала теория Гуи — Штерна оказалась вполне пригодной, то при попытке использовать ее для количественной интерпретации воз­никли серьезные трудности.

Измерение электропроводности растворов

Электропроводность электролитов обычно определяется при помощи мостовой схемы, используемой для измерения сопротивле­ния проводников I рода. В случае растворов электролитов приме­няют мосты, работающие на переменном токе, так как прохожде­ние постоянного тока через растворы приводит к значительным ошибкам, связанным с явлениями электролиза и поляризации. Необходимость применения переменного тока достаточно высокой частоты (для избежания указанных ошибок) усложняет измеритель­ную схему. Кроме моста, она включает в себя генератор перемен­ного тока, а также специальные устройства для выпрямления тока перед прохождением его через нуль-инструмент и для компенсации емкостных эффектов. Современные установки по измерению элек­тропроводности электролитов, в которых учтены все особенности проводников II рода, позволяют получать надежные результаты.

Вычислим потенциал течения. На рисунке приведена плоская поверхность твердого тела, относительно которой течет жидкость со постоянной скоростью u в направлении оси y, ось x нормальна к плоскости. Плоскость скольжения жидкости расположена на глубине , на уровне прилипшего слоя.

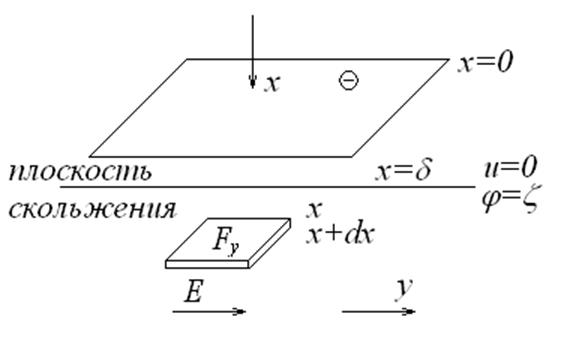
На границе твердого тела с жидкостью существует двойной слой, и поэтому потенциал изменяется вдоль оси x по некоторому закону. Жидкость при движении сносит заряд из двойного слоя и поэтому появляется электрическое поле E_y. Распределение потециала и скорости течения в направлении оси x приведено на рис. 

 

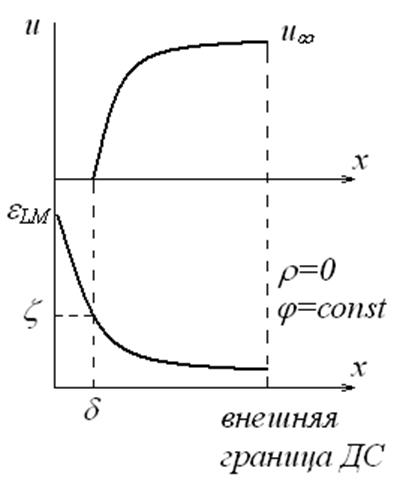
     Электрическая сила, действующая на слой уравновешивается силой вязкого сопротивления, равной в соответствии с уравнением Навье Стокса в одномерном случае произведению вязкости на вторую производную скорости течения u. Поскольку скорость и электрическое поле изменяются только в направлении нормальном стенке можно записать:

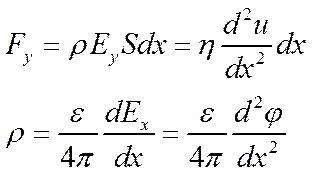
Подставляя заряд в выражение для силы получим результирующее уравнение:

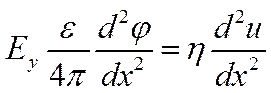
Краевые условия вдали от стенки:

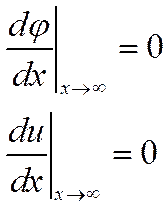
После первого интегрирования:

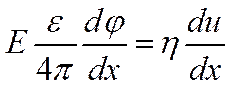
На плоскости скольжения x=d, потенциал равен дзета потенциалу течения j=z, а скорость равна нулю u=0

После второго интегрирования:

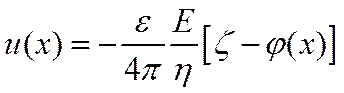
Поскольку на внешней границе ДС  можно считать φ=0, то

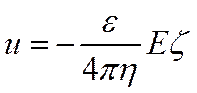
По определению z < e_LM

В общем случае z=f(x), h=h(x) и тогда