Химия \ Физическая химия

Электропроводность электролитов. Диффузия в электролитах. Компьютерное моделирование ионной атмосферы, страница 12

     По Изгарышеву, у обращенной к раствору поверхности металла можно найти и ионы металла, и адсорбированные молекулы воды (рис. 29). Ионы металла могут переходить из водной фазы в металлическую, теряя при этом свою гидратную оболочку и входя в состав кристаллической решет­ки. В то же время молекулы воды (или другого растворителя), адсорбируясь и ориентируясь определенным образом на границе раздела двух фаз, могут взаимо­действовать с ионами, находящимися в  металле,  и  при известных условиях   вырывать их из металли­ческой решетки. Следовательно, величина электродного потенциала

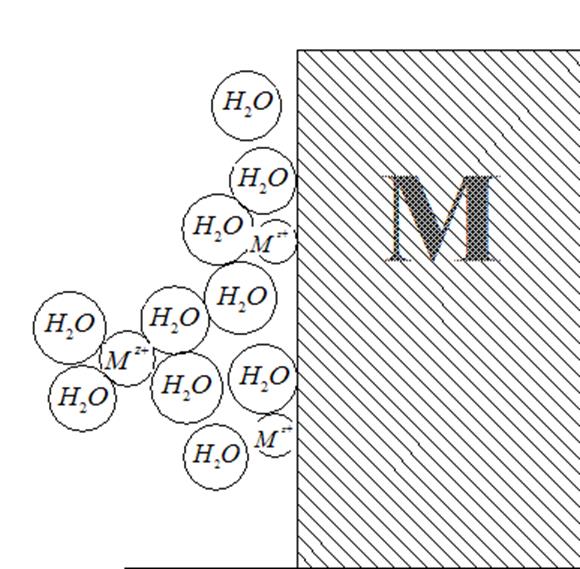
Рис. 29. Модель пограничного слоя металл-раствор при возникновении скачка потенциала на этой границе, по Н.А. Изгарышеву

должна зависеть от прочности связи иона в металле и энергии гидратации иона.

Рассмотрим границу металл – раствор. Следуя Герни, будем считать, что вероятность перехода метал­лического иона из раствора на металл (прямой переход) пропор­циональна числу металлических ионов, контактирующих со сторо­ны раствора с поверхностью металла (рис. 29), а вероятность обрат­ных переходов пропорциональна числу молекул растворителя, находящихся на поверхности металла. Герни полагал, что если nL— число молекул растворителя, a Nm — число ионов во всем объеме раствора, то для числа прямых переходов  и обратных перехо­дов  можно написать

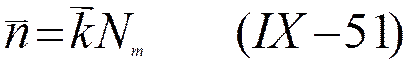
и

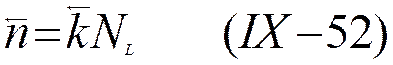
Так как энергетические уровни иона в растворе и в металле неодинаковы, то коэффициенты пропорциональности  и  должны быть функциями изменения энергии при переходе иона из одной фазы в другую. Эти изменения энергии можно оценить при помощи диаграммы, представленной на рис. 30. Здесь левая потенциальная кривая отвечает изменению свободной энергии иона как функции расстояния между ионом и гидратирующими его молекулами воды; положение молекул воды считается при этом заданным и отмечено пунктирной вертикальной линией. Горизонталь uL соответствует низшему колебательному уровню иона в растворе, горизонталь U0 — энергетическому уровню свободного газообразного иона. Правая потенциальная кривая показывает изменение энергии металличе­ского иона как функции его расстояния от неподвижной поверхности металла. Горизонталь Um на этой кривой отвечает низшему коле­бательному уровню иона в поверхностном слое металлической решетки. Для прямого перехода ион должен обладать таким запасом энергии,  который позволил бы ему подняться с уровня uL на уровень U0  (обозначим это количество энергии через ). Тогда

и  можно рассматривать как энергию вырывания иона из раство­ра. Ион, совершающий обратный переход, должен подняться с уров­ня Um на уровень U0. Пусть

тогда  будет энергией, необходимой для проведения этого про­цесса; ее можно определить как работу выхода иона из металла.

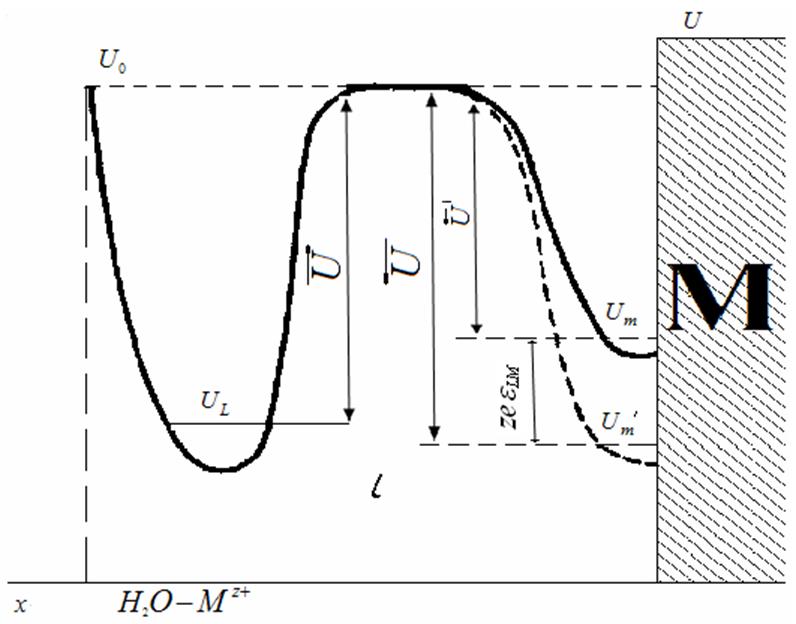
 Рис. 30. Потенциальная диаграмма Герни

Предположив, что к распределению ионов по энергетическим уров­ням применима статистика Максвелла — Больцмана, можно вместо (IX-51) и (IX-52) написать уравнения, в которых учтено изменение энергии иона при его прямых и обратных переходах

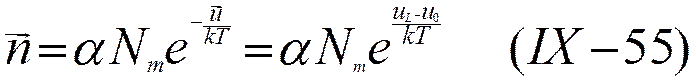
и

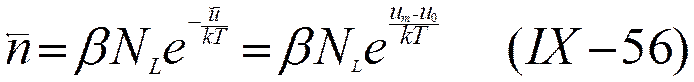
где α и β — факторы вероятности перехода.

Обычно в момент погружения металла в раствор , т. е. наблюдается преимущественный переход ионов в одном направле­нии. В результате этого возникает скачок потенциала между метал­лом и раствором, который, в свою очередь, изменяет энергетические состояния ионов. С течением времени, при достижении равновесия, частоты переходов ионов в обоих направлениях выравниваются

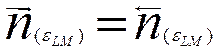
где eLM—равновесный скачок потенциала между металлом и раство­ром.

Предположим, следуя Герни, что энергия, связанная с возник­шим потенциалом, изменит энергетическое состояние ионов, распо­ложенных на поверхности металла. В этом случае уровень Um  опустится на величину zeeLM , как это показано на рис. 30 пунктир­ной кривой. Число обратных переходов тогда определится урав­нением

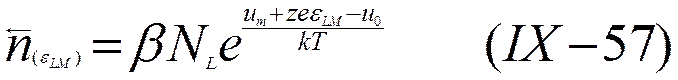
Поскольку 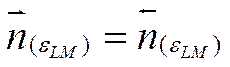, то

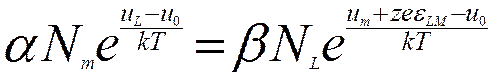
и

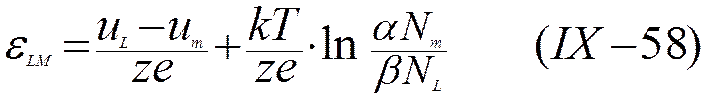
Уравнение (IХ-58) передает зависимость скачка потенциала металл — раствор от соотношения низших колебательных уровней металлического иона в растворе и металле, а также от концентра­ции раствора. Отношение числа растворенных частиц к числу молекул растворителя   Nm/NL  можно   рассматривать как величину, пропорциональную концентрации, выраженной, например, в г·ион/л. Как следует из уравнения (IX-53) и (IX-54), а также из рис. 30,

Скачать файл