природы ![]() –
является интегралом движения и представляет полную энергию осциллятора.
–
является интегралом движения и представляет полную энергию осциллятора.
3.2.2.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА 1. Вертикальный цилиндр, имеющий поперечные сечения
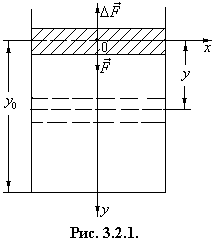
S = 80 см2 закрывается поршнем массы М = 1 кг. Объем цилиндра под поршнем V0 = 5 л. В начальный момент времени давление Р0 воздуха в цилиндре равнялось атмосферному. Каким будет закон движения поршня, если его сразу отпустить? Трение между поршнем и цилиндром отсутствует. Сжатие и расширение воздуха в цилиндре считать адиабатическим, смещение поршня – малым (рис.3.2.1)
|
ДАНО: S = 80 см2 М = 1 кг V0 = 5 л
|
СИ
|
АНАЛИЗ. Задача на динамику гармонических колебаний воздуха в цилиндре поршня при его малых перемещениях под действием двух сил: силы тяжести и переменной по закону адиабаты силы давления. РЕШЕНИЕ. При смещении
столба газа на величину у возникает сила
направленная в сторону, противоположную движению. |
|
|
 (рис.3.2.1). Уравнение
движения поршня имеет вид
(рис.3.2.1). Уравнение
движения поршня имеет вид ![]() , а в проекции на
ось оу:
, а в проекции на
ось оу:
![]() . (3.2.7)
. (3.2.7)
Сила Архимеда в данной задаче не
учитывается вследствие малости. Задача сводится к определению адиабатического
изменения давления ![]() . Запишем уравнение адиабаты
. Запишем уравнение адиабаты
![]() (3.2.8)
(3.2.8)
где v - объем газа, ![]() (i – число степеней свободы). Для воздуха (двухатомный
газ)
(i – число степеней свободы). Для воздуха (двухатомный
газ)
i
= 5, и g = 7/5. Чтобы найти
изменение давления ![]() , продифференцируем
(3.2.8):
, продифференцируем
(3.2.8): ![]() , отсюда
, отсюда ![]() .
Для конечных изменений давления
.
Для конечных изменений давления ![]() и объема
и объема ![]() с учетом начальных условий: t = 0,
с учетом начальных условий: t = 0,
P = P0,![]() , имеем:
, имеем: ![]() ,
,
![]() (3.2.9)
(3.2.9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.