Примеры решения задач по механике, страница 5

Учитывая начальные условия, t = 0, q₁= U₀ C, , получим А = CU₀,

j₁= 0. Получаем уравнение, которое описывает процесс изменения заряда q₁: . Закон изменения заряда q₂= q₀ - q₁ или q₂ = CU₀ - q₁ имеет вид .

ОТВЕТ: ; .

ЗАДАЧА 4. Определить период малых колебаний шарика, подвешенного на нерастяжимой нити длины см, если он находится в жидкости, плотность которой в n = 3 раза меньше плотности шарика. Считать сопротивление шарика пренебрежимо малым.

ДАНО:

см

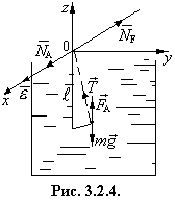
АНАЛИЗ. Задача на динамику гармонических колебаний шарика под действием силы тяжести, силы Архимеда и силы реакции - натяжения нити при отсутствии вязкости жидкости, в которую помещен колеблющийся шарик. При решении необходимо использовать уравнение динамики

Т – ?

вращательного движения

РЕШЕНИЕ. Для получения уравнения колебаний воспользуемся уравнением динамики вращательного движения:

, (3.2.24)

т.к. движение шарика можно считать вращательным относительно точки подвеса О. В законе (3.2.24) J – момент инерции материальной точки относительно точки подвеса О, – угловое ускорение материальной точки, – момент силы относительно точки подвеса. В задаче не приведены размеры шарика, следовательно, его можно представить как материальную точку.

На шарик в жидкости действуют: сила тяжести , сила Архимеда , натяжение нити . Найдем моменты этих сил относительно точки О. Модуль момента силы определяется углом a между векторами . Для силы тяжести и силы Архимеда (рис.3.2.4) , для силы натяжения нити , то есть . Момент силы тяжести действует в направлении, противоположном оси Оx согласно определению и равен по модулю, для малых углов , тогда .