ЗАДАЧА 8. Два стальных
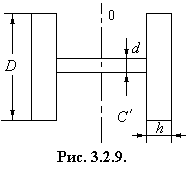
диска диаметром D = 0,8 м и толщиной h = 0,10 м плотно насажены на
стальную ось диаметром d =5 см и длиной 
= 2 м (см. рис.3.2.9.).
Найти период крутильных колебаний.
|
ДАНО: D = 0,8 м h = 0,10 м d = 5 см
|
АНАЛИЗ. Задача на определение периода крутильных колебаний. РЕШЕНИЕ: Из
симметрии фигуры следует, что ее недеформированное сечение располагается
посередине и поэтому при решении следует рассматривать в отдельности два
одинаковых крутильных маятника с длиной |
|
|
; 
,
где 
[Н×м×с2] –
момент инерции диска, 
[Н×м]
– коэффициент жесткости оси. Отсюда период крутильных колебаний равен 
с, т.к. 
.
ОТВЕТ: 
с.
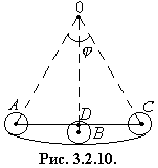
ЗАДАЧА 9. Шарик радиусом r скатывается по сферической поверхности из точки А (см. рис.3.2.10.). Определить радиус кривизны поверхности, если
АD = а, период колебаний Т0.
|
ДАНО: r АD = а Т0 |
АНАЛИЗ. Если угол j достаточно мал, то скатывающийся шарик будет совершать гармонические колебания. Это возможно в случае, когда R>>DB, а амплитуда колебаний при этом будет достаточно мала. При этом дугу АВ можно считать хордой. |
|
|
РЕШЕНИЕ:
Определим сначала радиус кривизны R траектории
центра шарика. Будем считать, что шарик совершает незатухающие колебания с малой
амплитудой, с периодом Т0 по закону:
, (3.2.42)
где а = АD – амплитуда колебаний шарика, если считать, что дуга АВ близка по величине хорде. Продифференцировав (3.2.42),
.
(3.2.43)
Для решения задачи воспользуемся законом сохранения энергии, учитывая при этом, что шарик при движении по поверхности вращается вокруг собственного центра масс:
,
(3.2.44)
где V
– линейная, w – вращательная
скорости шарика; J –
момент инерции шарика относительно центра масс, т.е. 
,
, где r
– радиус шарика. После подстановки w
и J в (3.2.44)
получим 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
.
Дифференциальное уравнение колебаний любого из них имеет вид:
