Примеры решения задач по механике, страница 7

 теореме  Штейнера J = J₀+m₀ х², т.е.  

                             .                (3.2.28)

Стержень вращается относительно закрепленной оси, поэтому для определения характера его движения следует использовать основное уравнение динамики вращательного движения:

                     .                      (3.2.29)

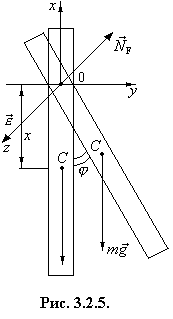
Вектор углового ускорения  направлен вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта. (см. рис.3.2.5). Во время движения на стержень действуют сила тяжести  и сила реакции оси. Вращающий момент силы реакции оси равен нулю, т.к. . Вращающий момент относительно оси (точка 0 на рис.3.2.5) создает только сила тяжести:  Момент  направлен в сторону, противоположную вектору  и по модулю равен: , т.к. j – мал, и sin j » j.

          В проекции на ось Оx уравнение (3.2.29) запишется

                                                ,                                                (3.2.30)

где J определяется из равенства (3.2.28). Момент силы, действующий на стержень, прямо пропорционален угловому смещению и поворачивает стержень к положению равновесия. Уравнение (3.2.30) можно рассматривать как уравнение колебаний (3.2.1). Подставим в (3.2.30) значение J из (3.2.28):

. Величина , ее обозначают w₀², тогда получим дифференциальное уравнение колебаний:

                                                          ,                                           (3.2.31)

где                                            .                           (3.2.32)

Уравнение (3.2.31) – линейное однородное дифференциальное уравнение с постоянными коэффициентами. Решение находят, составляя соответствующее характеристическое  уравнение r² +w₀² = 0. Корни уравнения мнимые , решение имеет вид  , или в тригонометрической форме:

j = А cos(w ₀ t+a), w₀    определяется из выражения (3.2.32).

          Стержень совершает малые гармонические колебания с частотой

; период колебаний стержня

                                 ,                                (3.2.33)

Т₀= 1,58 с, если = 1 м, х = 0,2 м.

          Рассмотрим характер зависимости Т(х). Величина х  согласно условиям задачи изменяется в пределах от 0 до / 2. При х = 0, Т® ¥, т.е. стержень находится в состоянии безразличного равновесия и не совершает колебаний, когда ось вращения совпадает с центром масс стержня.