В точке А потенциальная энергия шарика максимальна (DВ = h), кинетическая равна нулю. В точке В потенциальная полностью переходит в кинетическую энергию, которая достигает максимальной величины
![]() . (3.2.45)
. (3.2.45)
Значение
Vmax определим из выражения (3.2.43): ![]() .
Подставим значение Vmax в (3.2.45), получим
.
Подставим значение Vmax в (3.2.45), получим ![]() ,
,
![]() (3.2.46)
(3.2.46)
Выразим величину h через радиус кривизны R.
Из треугольника АDО по теореме Пифагора имеем R2 =
a2 + (R - h)2, a2= 2Rh - h2.
Получим квадратное уравнение относительно h: h2– 2R h - a2= 0. Корни
уравнения ![]() . Корень
. Корень ![]() дает
значение h2 > R, что в данной
задаче не имеет физического смысла. Корень
дает
значение h2 > R, что в данной
задаче не имеет физического смысла. Корень ![]() подставим
в выражение (3.2.46):
подставим
в выражение (3.2.46): ![]() =
=![]() , отсюда
, отсюда
![]() .
.
Радиус кривизны поверхности ![]() , тогда
, тогда
![]() .
.
ОТВЕТ: ![]() .
.
ЗАДАЧА 10. Найти
частоту свободных колебаний электрона в атоме водорода ![]() ,
считая, что положительный его заряд сосредоточен в объеме радиусом r =10-15 м, а
электронный заряд q распределен по сфере с
боровским радиусом а = 5×10-12
м. Принять, что плотность электронного заряда внутри указанной сферы постоянна.
,
считая, что положительный его заряд сосредоточен в объеме радиусом r =10-15 м, а
электронный заряд q распределен по сфере с
боровским радиусом а = 5×10-12
м. Принять, что плотность электронного заряда внутри указанной сферы постоянна.
|
ДАНО:
r =10-15 м а = 5×10-12 м q,
|
АНАЛИЗ. Задача на динамику электромагнитных колебаний. В невозмущенном состоянии ядро атома водорода можно считать точечным и расположенным в центре сферы радиуса а, внутри которой согласно классическим предположениям распределение заряда будет равномерным с объемной плотностью r. РЕШЕНИЕ. В невозмущенном состоянии ядро атома водорода можно считать точечным. Оно находится в центре |
|
|
 сферы радиуса а,
внутри которой согласно классическим предположениям равномерно распределен
заряд с объемной плотностью r.
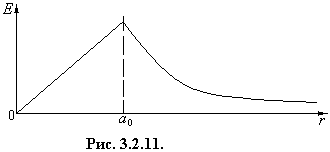
(см. рис.3.2.11.).
сферы радиуса а,
внутри которой согласно классическим предположениям равномерно распределен
заряд с объемной плотностью r.
(см. рис.3.2.11.).
Смещаясь из центра 0, ядро оказывается в точке, напряженность электрического поля которой можно найти из теоремы Гаусса для области, когда r < a:
![]() (3.2.47)
(3.2.47)
![]() ,
,
![]() на поверхности сферы радиуса r, и тогда (3.2.47) примет вид:
на поверхности сферы радиуса r, и тогда (3.2.47) примет вид: ![]() , где
, где ![]() .
В результате имеем
.
В результате имеем ![]() (см. рис.3.2.11). Таким
образом, на электрон в поле ядра действует сила
(см. рис.3.2.11). Таким
образом, на электрон в поле ядра действует сила ![]() ,
т.е.
,
т.е. ![]() – квазиупругая сила,
пропорциональная смещению r и
направленная в сторону равновесия.
– квазиупругая сила,
пропорциональная смещению r и
направленная в сторону равновесия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.