|
ДАНО:
|
АНАЛИЗ. Задача на упругие колебания стержня вокруг вертикальной оси, проходящей через неподвижный центр стержня. Незначительность угла предварительного поворота стержня позволяет считать последующие за этим колебания с малой амплитудой гармоническими. |
|
|
 РЕШЕНИЕ.
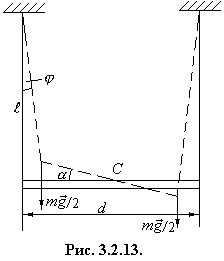
Стержень повернули на малый угол a
вокруг вертикальной оси, проходящей через центр масс стержня. При этом нить
отклонилась на угол j, причем
РЕШЕНИЕ.
Стержень повернули на малый угол a
вокруг вертикальной оси, проходящей через центр масс стержня. При этом нить
отклонилась на угол j, причем ![]() , т.е.
, т.е.
![]() ,
(3.2.47)
,
(3.2.47)
где d – длина стержня.
После того как нить
отпустили, стержень начал совершать малые колебания. Уравнение колебаний имеет
вид: ![]() , т.к. для малых колебаний
, т.к. для малых колебаний ![]() , возвращающий момент силы
, возвращающий момент силы ![]() . Учитывая (3.2.47), получим
. Учитывая (3.2.47), получим ![]() , где I
– момент инерции стержня относительно точки С, т.е.
, где I
– момент инерции стержня относительно точки С, т.е. ![]() .
В результате
.
В результате
![]() ,
далее
,
далее ![]() . Обозначим
. Обозначим ![]() .
Уравнение колебаний имеют вид:
.
Уравнение колебаний имеют вид: ![]() , где
, где ![]() , а
, а ![]() с.
с.
ОТВЕТ: ![]() с.
с.
3.2.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Маятник состоит из медной проволоки диаметром d1 = 0,1 мм и медного шарика диаметром d2 = 3 см. На сколько процентов увеличится период колебания, если заменить медный шарик свинцовым того же диаметра. Амплитуду считать малой.
2. Шар, радиус которого
r = 5 см подвешен на
нити длиной ![]() см. Определить погрешность, которую
мы делаем, приняв его за математический маятник с длиной
см. Определить погрешность, которую
мы делаем, приняв его за математический маятник с длиной ![]() =15 см.
=15 см.
3. Некоторое тело
качается около оси с периодом Т1 = 0,5 с. Если же к нему
прикрепить грузик с массой m = 50 г на
расстоянии ![]() см ниже оси, то оно качается с
периодом Т2 = 0,6 с. Найти момент инерции тела относительно
оси качания.
см ниже оси, то оно качается с
периодом Т2 = 0,6 с. Найти момент инерции тела относительно
оси качания.
4.Определить период колебаний массы m = 121 г ртути, находящейся в U – образной трубке. Площадь сечения трубки S = 0,3 см2.
5. Шарик катается по дну сферической чашки. Предполагая, что эти колебания можно считать синусоидальными, определить их период. Считать радиус чашки равным R, радиус шарика r.
6. Предположим, что по одному из диаметров Земли просверлена шахта. Принимая Землю за однородный шар с плотностью r = 5,5×103 кг/м3: а) показать, что при отсутствии трения тело, падающее в этой шахте, совершает гармонические движения; б) найти время t движения тела от поверхности Земли до ее центра.
7. Два диска могут вращаться около осей, являющихся продолжением одна другой. Моменты инерции дисков относительно этой оси равны J1 и J2. Диски соединены пружиной, коэффициент кручения которой равен G. Определить период, с которым будут колебаться диски, если их повернуть в противоположных направлениях, закручивая при этом пружину, и отпустить.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.