Примеры решения задач по механике, страница 15

          8. Определить период колебаний переднего колеса велосипеда, поднятого в вертикальное положение. Колесо состоит из обода, массу которого т = 3 кг можно считать равномерно распределенной по окружности с радиусом R = 35 см и из укрепленного на ободе вентиля (т₂ = 50 г). Моментом инерции спиц и втулки пренебречь.

          9. Тело неподвижно висящее на цилиндрической пружине, растягивает ее на х₀ = 5,0 см. Затем тело было смещено из положения равновесия по вертикали и отпущено. Описать характер движения тела. Найти период колебаний.

          10. Маятник длиной  см колеблется в кабине самолета. Каков период его колебаний а) если самолет движется равномерно; б) если самолет движется горизонтально с ускорением  а = 2,5 м/с²; в) если самолет планирует вниз под углом a = 15⁰ к горизонту. Лобовым сопротивлением самолета пренебречь.

          11. Часы, ход которых регулируется физическим секундным маятником, точно идут на Земле. Определить поправку за час для этих же часов, помещенных на Луне.

          12. Математический  маятник массой т = 100 г и длиной  м совершает гармонические колебания по закону . Определить натяжение в момент времени t = T / 2.

          13. Стенные часы, ход которых регулируется математическим секундным маятником, точно идут на широте Москвы. Определить  поправку за сутки для этих часов на экваторе.

          14. Определить момент инерции тела массы т = 40 кг, совершающего колебания с периодом Т =3,14 с, если расстояние от точки подвеса до центра тяжести  м.

          15. Тело массой т совершает колебания по закону х = х₀sinw t. Определить силу, действующую на тело и его максимальную кинетическую энергию.

          16. Тело движется под действием силы по закону . Найти работу силы за время от  t = t_Н  до t = t_К. Найти работу силы за один период действия силы и среднюю мощность  за тот же период.

          17. На тело действует сила, изменяющаяся по закону  (А и w – постоянные числа). Найти закон движения тела  при условии, что при t = 0, х = 0, V = 0. Установить, что такое движение является колебательным. Определить период колебания, наибольшее значение х (t) и наибольшее значение скорости.

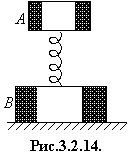
          18. Тело А массы т₁ = 1,00 кг и тело В массы т₂ = 4,10 кг соединены между собой пружиной (рис.3.2.14.). Тело А совершает свободные вертикальные гармонические колебания с амплитудой а = 1,6 см и частотой w =25 с^-1. Пренебрегая массой пружины, найти наибольшее и наименьшее значения силы давления этой системы на опорную плоскость.

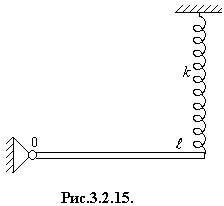          19. Однородный стержень массы т совершает малые колебания вокруг горизонтальной оси, проходящей через точку О (рис.3.2.15). Правый конец стержня подвешен на невесомой пружине жесткости k. Найти период колебаний стержня, если в положении равновесия он горизонтален.

          20. Два шара с массами т₁ = 1,0 кг и т₂ = 2,0 кг насаже6ны на гладкий горизонтальный стержень. Шары связаны друг с другом легкой пружинкой с жесткостью k = 24 Н/м. Левому шару сообщили начальную скорость V₁ = 12 см/с. Найти: а) частоту колебаний системы в процессе движения; б) энергию и амплитуду колебаний.