Примеры решения задач по механике, страница 4

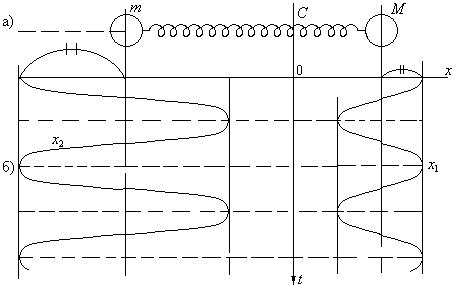
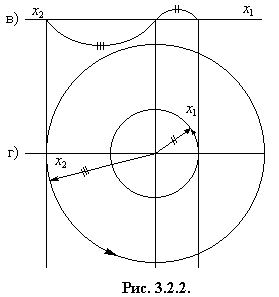
          ОТВЕТ: Колебания осциллятора происходят с той же частотой, что и для осциллятора с приведенной массой m. Колебания обеих масс происходят в противофазе. На рис.3.2.2, б изображена  развертка колебаний во времени. Центр масс системы неподвижен. На рис.3.2.2, в изображена векторная диаграмма колебаний. Видно, что амплитуда колебаний массы М меньше амплитуды колебаний меньшей массы  т. Фазовая траектория колебания масс М и т представляют собой окружности, причем R_M <R_m (рис.3.2.2, г).

          ЗАДАЧА 3. Цепь состоит из соединенных последовательно  двух одинаковых конденсаторов емкостью С и катушки с индуктивностью L (рис.3.2.3). Между конденсаторами включен ключ. При разомкнутом ключе К один из конденсаторов заряжают до напряжения U₀ и отключают источник напряжения. Найти закон изменения зарядов конденсаторов со временем после замыкания ключа.

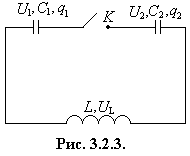Этот заряд после замыкания ключа К (рис.3.2.3) распределяется между двумя одинаковыми конденсаторами. 

Из закона сохранения заряда следует:

           q₁ + q₂ = q₀, или q₁ + q₂= CU₀,              (3.2.22)

Продифференцируем равенство (3.2.22):

, отсюда ,

где I – ток, протекающий в цепи.  Заряд q₁ со временем уменьшается, q₂  – увеличивается. По цепи протекает ток I , который периодически изменяет направление. Чтобы записать уравнение колебаний, воспользуемся правилом Кирхгофа:

                                        U_L + U_C + U_C = 0                                               (3.2.23)

Учтем, что (Закон Фарадея); , т.к.  и . Подставим значения U_L  и  U_C в равенство (3.2.23):

 или , тогда получим  или  ,        т.к., то , т.е.

Получим уравнение  уравнением колебания (3.2.1) для рассматриваемого колебательного контура. Его решением является гармоническая функция