Программа, контрольные задания и методические рекомендации для студентов специальностей 1706, 2713, 2102 заочной полной и сокращенной форм обучения, страница 9

Пример К1. Даны уравнения движения точки в плоскости :

,

(- в см,   - в с).

Определить:

·  Уравнение траектории точки;

·  Скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны траектории при  с.

Решение:

1.  Для определения уравнения траектории точки  необходимо исключить из заданных уравнений движения время . Поскольку  входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу;

   или   ,      (1)

Из уравнений движения находим выражения функций:

,  

Полученные значения функций подставляем в равенство (1).

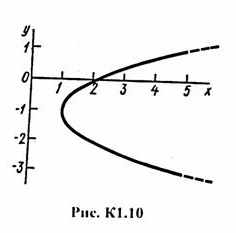
Отсюда окончательно находим следующее уравнение траектории точки парабола (рис. К1.10):

2.  Скорость точки найдем по ее проекциям на координатные оси:

при  с,  см/с,  см/с,  см

3.  Аналогично найдем ускорение точки

; ;

и при  с:

 см/с²,  см/с²,  см/с²

4.  Касательное ускорение  найдем, дифференцируя по времени равенство . Получим

 и

Числовые значения величин , , , , входящих в правую часть выражения, определены выше. Подставив эти значения, найдем, что при  с,  см/с².

5.  Нормальное ускорение точки найдем из равенства , откуда . Подставляя найденные числовые значения  и , получим, что при  с,  см/с².