Программа, контрольные задания и методические рекомендации для студентов специальностей 1706, 2713, 2102 заочной полной и сокращенной форм обучения, страница 13

 - известная скорость точки этого тела;

 - мгновенный центр скоростей (мгновенный центр вращения);

 - угловая скорость тела относительно центра ;

              ,  - расстояние точек  и  от центра  (мгновенные радиусы).

              Вектор искомой скорости  перпендикулярен мгновенному радиусу . При определении угловой скорости звена следует использовать свойство, что скорость вращения звена в плоскости по модулю и направлению равна угловой скорости звена относительно мгновенного центра скоростей

              Для определения ускорений точек механизма следует использовать векторное равенство

; , (1)

где:  - точка, ускорение которой известно по условиям задачи или определено при решении задачи ранее;  - точка, ускорение которой надо найти.

              При решении задач модуль ускорения  может быть определен по формулам:

 или

              ,  находятся из уравнения (1), записанного в проекциях на оси координат , .

              Угловое ускорение звена определяем из соотношения

Например

Пример решения задачи

              Плоский механизм (рис. К2.11) состоит из стержней 1, 2, 3 и ползунов , , соединенных друг с другом и с неподвижной опорой  шарнирами.

              Определить скорости ползунов , , угловую скорость звена , ускорение точки  и угловое ускорение звена .

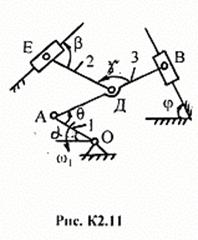
Дано:  м,  м, .

, , , , ,  1/с,  1/с².

Определить: , , , , .