Методические указания.
Задача решается исходя из условия равновесия механической системы при действии на нее произвольной пространственной системы сил.
Порядок решения задачи.
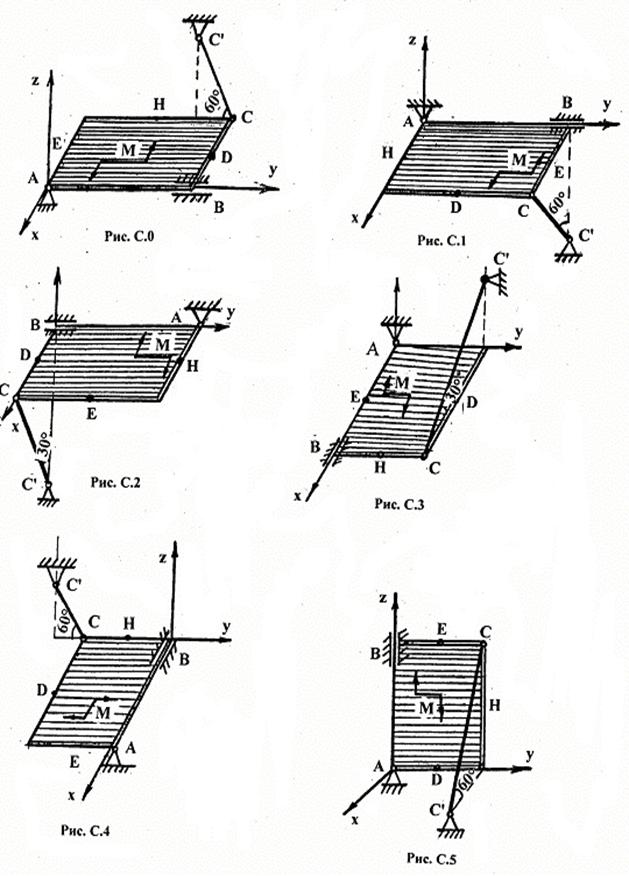
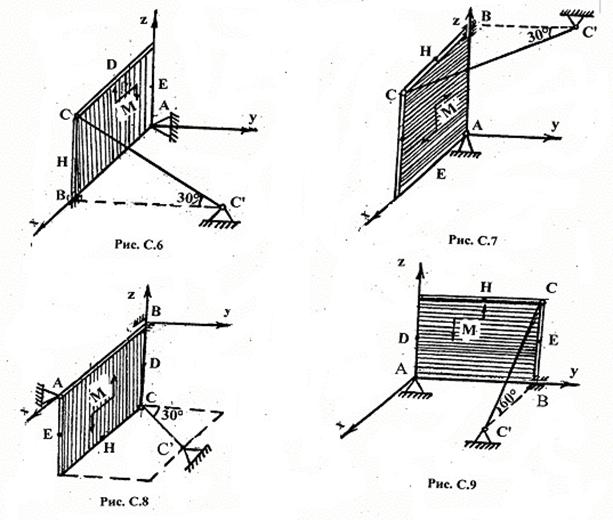
1. Изобразить схему механической системы, показать действующие на нее силы согласно условию задачи.
2.
Выделить тело или группу тел,
равновесие которых будет рассматриваться. Провести оси координат ![]() .
.
3. Заменить действие связей соответствующими реакциями.
4. Преобразовать полученную систему сил к виду, удобному для составления уравнений равновесия: силы, направленные под углом к осям координат, разложить на составляющие, параллельные осям.
![]() .
.
где ![]() - углы между
направлениями вектора
- углы между
направлениями вектора ![]() и направлениями
и направлениями ![]() соответственно.
соответственно.
5. Составить шесть уравнений равновесия.
6. Решить полученную систему уравнений относительно неизвестных реакций, провести анализ результатов решения.
При выделении тела, равновесие которого будет рассматриваться, необходимо учитывать, чтобы число неизвестных реакций связей, наложенных на это тело, соответствовало числу уравнений равновесия.
При составлении уравнений моментов относительно оси следует помнить, что момент силы перпендикулярной оси равен произведению модуля силы на кратчайшее расстояние между осью и линией действия силы (плечо силы). Знак момента можно определить по правилу: момент положителен, если сила «стремится» повернуть плечо относительно оси против хода часовой стрелки при виде на плечо с положительного направления оси. Момент силы относительно оси равен нулю, если линия действия силы параллельна оси или пересекается с осью.
Пример решения задачи.
Однородная прямоугольная плита весом ![]() закреплена сферическим шарниром в
точке
закреплена сферическим шарниром в
точке ![]() , цилиндрическим – в точке
, цилиндрическим – в точке ![]() и невесомым шарнирным стержнем
и невесомым шарнирным стержнем ![]() , расположенным в плоскости,
параллельной
, расположенным в плоскости,
параллельной ![]() . К плите приложена сила
. К плите приложена сила ![]() в плоскости
в плоскости ![]() и
пара сил в плоскости
и
пара сил в плоскости ![]() с моментом
с моментом ![]() . Точка приложения силы, направление
силы, линейные размеры плиты показаны на схеме. Определить реакции связей в
точках
. Точка приложения силы, направление
силы, линейные размеры плиты показаны на схеме. Определить реакции связей в
точках ![]() .
.
Дано: ![]() кН,
кН, ![]() кН,
кН, ![]() кНм,
кНм,
![]() ,
, ![]() м.
м.
Определить: реакции в точках ![]()
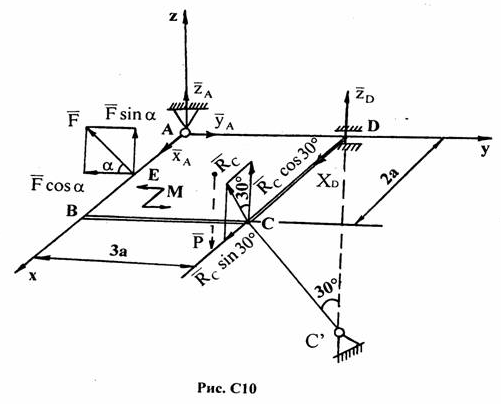
Решение.
1. Изобразим схему плиты с опорами и действующие на нее силы в соответствии с условием задачи (Рис. С10).
2.
Для определения реакций в точках ![]() рассмотрим равновесие плиты
рассмотрим равновесие плиты ![]() .
.
3.
Покажем на схеме реакции связей.
Реакцию неподвижного сферического шарнира представим в виде трех составляющих ![]() ,
, ![]() ,
, ![]() , реакцию цилиндрического шарнира –
двумя составляющими
, реакцию цилиндрического шарнира –
двумя составляющими ![]() , реакцию
, реакцию ![]() невесомого стержня.
невесомого стержня.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.