Программа, контрольные задания и методические рекомендации для студентов специальностей 1706, 2713, 2102 заочной полной и сокращенной форм обучения, страница 24

Методические указания

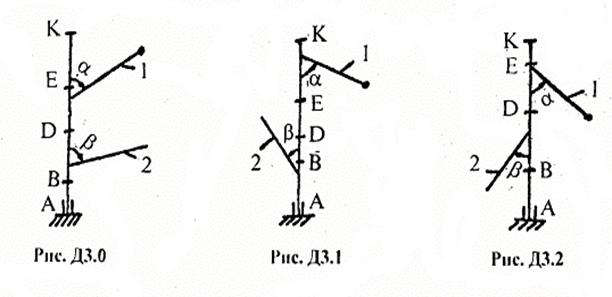
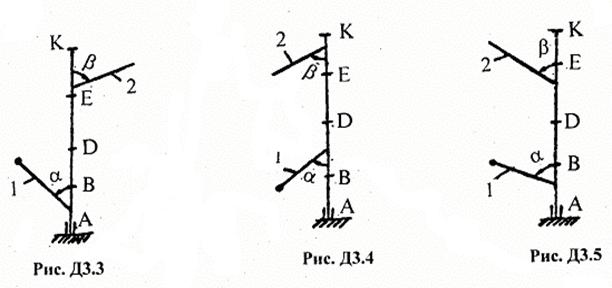
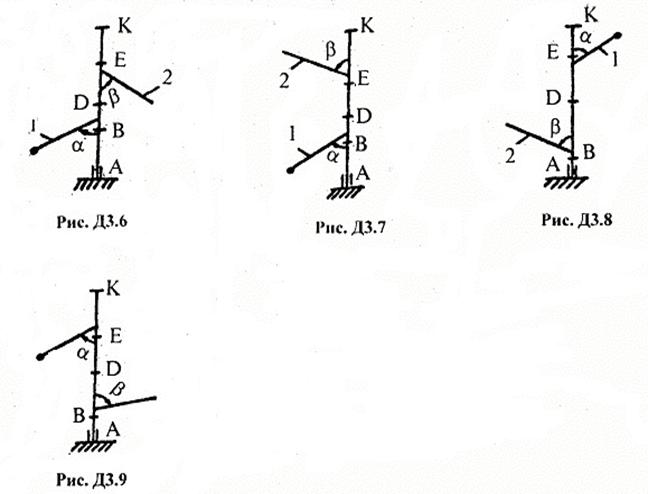
Задача Д3 – на применение к изучению движения системы принципа Даламбера.

Принцип заключается в следующем: если к действующим на механическую систему внешним силам присоединить силы инерции, то полученная система сил будет уравновешенной, т.е.

(1),

где: - внешняя сила, - сила инерции.

Применение уравнения (1) упрощает решение задач динамики. По существу, это уравнение эквивалентно уравнению равновесия статики.

При действии одной материальной точки на другую силой возникает сила противодействия, равная по модулю и противоположно направленная силе . Эта сила возникает вследствие свойства инерции материальных тел и называется силой инерции .

Таким образом , или с учетом .

При движении твердых тел с ускорением возникает система распределенных сил инерции. В этом случае целесообразно привести эти силы к некоторой точке.

1. Поступательное движение твердого тела

При поступательном движении все точки имеют одинаковые по модулю и направлению ускорения: , где - ускорение -ой точки тела, - ускорение центра масс тела. Тогда

где: - суммарная масса тела.

Следовательно, при поступательном движении твердого тела система сил инерции заменяется одной силой , приложенной в центре масс тела.

2. Вращательное движение твердого тела.

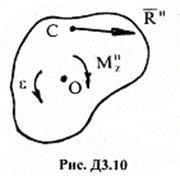
Если твердое тело имеет плоскость симметрии и вращается вокруг оси , перпендикулярной этой плоскости, то система сил инерции приводится к главному вектору и главному моменту этих сил (рис. Д3.10).