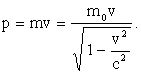
Законы механики сохраняют свой вид и в релятивистской динамике. Изменение импульса d(mv ) равно импульсу силы Fdt
dp = d(mv) = F dt.
Отсюда dp/dt = F- есть выражение основного закона релятивистской динамики для материальной точки.
В обоих случаях входящая в эти выражения масса является переменной величиной (m ≠ const) и ее также необходимо дифференцировать по времени.
Установим связь между массой и энергией. Возрастание энергии, так же как и в классической механике, вызывается работой силы F. Следовательно, dE = Fds. Разделив левую и правую части на dt, получим
Подставляем сюда 
.
Умножив левую и правую части полученного равенства на dt , получим 
Из
выражения для массы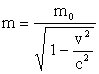 
определим
.
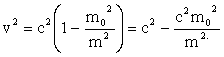Продифференцируем выражение v2.
Подставим
v2 и d(v2) в выражение для dE
Интегрируя это выражение, получим E = mc2.
Полная энергия системы Е равна произведению массы на квадрат скорости света в вакууме. Связь между энергией и импульсом для частиц не имеющих массы покоя в релятивистской динамике дается соотношением
E = pc,
которое легко получить математически: E =mc2 , p = mv. Возведем оба равенства в квадрат и обе части второго домножим на с2
E2 = m2 c4 , p2 c2 = m2 v2 c2 .
Вычтем почленно из первого равенства второе
E2 – p2 c2 = m2 c4-m2 v2 c2 = m2 c4 (1-v2 / c2 ).
Учитывая, что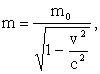 
получим
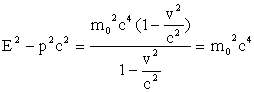
Так как масса покоя m0 и скорость света с величины, инвариантные к преобразованиям Лоренца, то соотношение (E2 - p2 c2 ) также инвариантно к преобразованиям Лоренца. Из этого соотношения получим выражение для полной энергии
Таким образом, из этого уравнения можно сделать вывод:
энергией обладают и материальные частицы, не имеющие массы покоя (фотоны, нейтрино). Для этих частиц формула связи энергии и импульса имеет вид E = pc.
Из приведенных выше преобразований получили dE=c2dm. Интегрирование левой части в пределах от E0 до Е, а правой от m0 до m, дает
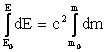
E – E0 = c2 (m – m0 ) = mc2 – m0 c2 ,
где E = mc2 - полная энергия материальной точки,
E0 =m0 c2 - энергия покоя материальной точки.
Разность Е – Е0 есть кинетическая энергия Т материальной точки.
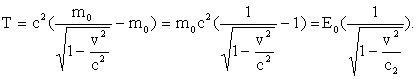
При
скоростях v « c , разложим 
в ряд:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.