Физика (Часть 1): Учебно-практическое пособие, страница 25

                              v_y  =  v'_y              v'_y   = v_y

                             v_z  =  v'_z             v'_z  = v_z .

Эти  соотношения носят название  правила сложения скоростей в классической механике.

Рассмотрим преобразование ускорений. Взяв вторую производную  от координаты по времени,  получим

,

т.е. ускорения  в обеих системах отсчета  равны между собой a_x=a'_x. Видно, что ускорение,   в отличие  от скорости, носит абсолютный  характер, т.е. ускорение   одного и  того же тела одинаково  во всех инерциальных системах отсчета.

Физические величины   и  физические законы, не  изменяющиеся при переходе от одной инерциальной системы к другой называют  инвариантными (неизменяющимися) к преобразованиям Галилея. А вот законы  электродинамики Максвелла оказались неинвариантными к преобразованиям Галилея.  Этот   парадокс    поставил   ученых   перед   выбором: 

а) отказаться от  уравнений Максвелла,  считая их  неправильными;  б) отбросить принцип относительности;  

в) считать преобразования Галилея неточными и заменить  их другими. Эйнштейн в 1905 г. и  Пуанкаре показали, что следует остановиться на последней  возможности. При выводе преобразований Эйнштейн исходил из 2-х постулатов:

1.Физические законы одинаковы во всех инерциальных системах отсчета, и, следовательно, математическая форма записи законов должна быть инвариантна к преобразованиям.

2. Скорость света в  вакууме одинакова во всех инерциальных системах и не  зависит от направления его  распространения  и движения источника и приемника.

Невозможно понять  как и почему (c + v) должно равняться  с.  Чтобы понять это, необходимо  отрешиться от  ньютоновских представлений об абсолютности пространства  и времени. Преобразования   координат и  времени, учитывающие  их зависимость  от скорости, называются  преобразованиями Лоренца и имеют  вид:

                                    

                                   

                                    

                          .

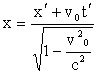
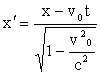
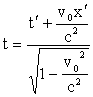
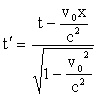Из  преобразований  видно:

1.  Время также поддается преобразованиям, что свидетельствует  об относительности времени.

2.  В формулах  преобразования время выступает как равноправная четвертая координата. Это означает, что в новой теории пространство и время неразделимы, т.е. взаимосвязаны.

Нетрудно видеть, что при v₀ /c « 1 преобразования Лоренца переходят в преобразования Галилея.

Пространство и время в специальной теории относительности.

Разберем некоторые особенности пространства и времени, вытекающие из преобразований Лоренца.

Относительность одновременности. В классической механике события, одновременные в одной какой-либо инерциальной системе отсчета ,  будут одновременными во всех других инерциальных системах. Иначе   обстоит дело в специальной теории относительности .

Пусть в движущейся со скоростью v₀ системе K′ в точках с  координатами   x′₁и  x′₂ одновременно  ( в момент t′ ) произошло два события   (например, зажглись две лампочки).  Эти же события в неподвижной системе отсчета K будут  происходить в разные моменты  времени t₁  и  t₂.  В самом деле, исходя  из  преобразований  Лоренца ,  получим