Физика (Часть 1): Учебно-практическое пособие, страница 20

уравнение динамики вращательного движения, или уравнение  II закона Ньютона для вращательного движения. Угловое ускорение прямо  пропорционально моменту силы и обратно пропорционально моменту инерции тела.

Момент инерции характеризует инерционность тела при  вращательном  движении и зависит не только от массы тела, но и от распределения этой массы относительно оси вращения. В  общем  случае, если  тело сплошное, оно представляет собой совокупность  множества точек с бесконечно малыми массами dm и момент инерции тела определяется интегралом

.

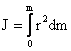Пределы интегрирования  определяются формами и размерами тела.

В  тех случаях, когда  ось  вращения  проходит через  центр тяжести (или центр инерции)  тела,  а  тело имеет  правильную   геометрическую форму , интегрированием легко получить выражения  для момента инерции  и  они являются наиболее  простыми. Так, момент инерции обруча,  кольца  и пустотелого  цилиндра  J = mR² ; диска  и  сплошного  цилиндра J =;  шара J = , стержня где m- масса тела,  R- радиус, ℓ-длина  стержня.

В   тех  случаях,   когда  ось вращения проходит  не  через   центр  инерции  тела,  момент  инерции  определяется  по теореме  Штейнера:

J =J₀  + md² .

Момент инерции J относительно произвольной  оси равен сумме момента  инерции J₀  относительно оси, параллельной  данной и проходящей через центр инерции   тела ,  и  произведения массы тела  m на квадрат расстояния  d  между осями.

Момент инерции J тонкого  стержня длиной  l относительно  оси  O΄ O΄, проходящей  через его конец (рис. 14а) . Момент инерции шара относительно оси O^’ O^’, касательной к его поверхности (рис.14б)

Кинетическая энергия и работа при вращательном движении.

Мысленно разобьем тело на малые частицы  с массами m₁, m₂ , …, m_n так, чтобы линейные скорости материальных точек составляющих эти частицы можно было считать одинаковыми. Расстояния  этих частиц от оси вращения, соответственно равны r₁, r₂, …, r_n , а скорости - v₁, v₂, …, v_n. Кинетическая энергия  каждой частицы будет   а  всего тела:

Заменим линейную скорость v_i ее выражением через угловую v_i = ωr_i.

.

Так как угловая скорость для всех  точек тела одинакова, т.е. ω=const, то

Выражение ,  стоящее в скобках, есть сумма моментов  инерции частиц  тела, т.е. момент инерции J, и тогда вырaжение для кинетической энергии   вращательного  движения примет вид

E= J∙ω² /2,

Если тело участвует в двух движениях одновременно - в поступательном со  скоростью v и вращательном со скоростью ω, то его полная кинетическая энергия равна

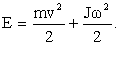
Работа внешней силы постоянной величины при вращении равна   ΔA = т.е.  равна произведению момента внешней силы на угол поворота . В общем случае dA = M dφ  и  работа будет