Физика (Часть 1): Учебно-практическое пособие, страница 19

За  время    Δt   тело повернется на угол  Δ φ  точка m пройдет путь Δs  =  r ∙ Δ φ.        Разделив обе части этого равенства на Δt и, переходя к пределу,  получим

   или   ,

v = r∙ω  , где ω = dφ/dt  - производная  от угла поворота φ по времени называется  угловой  скоростью. ω - измеряют в рад/с, или  с^-1 часто угловую скорость задают числом  оборотов n в единицу времени. Эти две   величины связаны отношением     ω = 2πn.

При неравномерном  вращении угловая  скорость  ω    изменяется со  временем и  за  время Δt  получает приращение  Δω. При этом   линейная  скорость  точки  также получает приращение Δv ,  равное

Δv= Δ (r∙ω) = r∙Δω.

Разделив обе  части  равенства на Δt,  и переходя к  пределу, получим     

   или   .

Производная dω/dt = ε   называется угловым ускорением,  а соотношение a_τ=r∙ε  выражает связь линейного тангенциального a_τ и углового ускорения. Угловое ускорение измеряют в рад/c² или  с^-2 .

Известно, что при  криволинейном движении тангенциальное ускорение  характеризует   изменение  скорости по  величине, а   нормальное – по   направлению и равно a_n = v²/r. Учитывая, что v= ωr, получим    связь  нормального  ускорения  с угловой  скоростью:

а_n  = ω²r.

Величина  полного  ускорения а, выраженная через  характеристики  вращательного движения, имеет вид

 При равнопеременном вращательном движении (ε  =  const) формулы для  определения угла  поворота  и угловой  скорости  имеют вид

                   .

Динамика вращательного движения

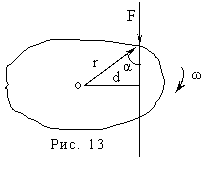                       Чтобы твердое тело с закрепленной осью привести во вращение, к нему необходимо приложить силу, не проходящую  через ось вращения и не параллельную ей.  Вращательное движение под действием силы F определяется не только ее величиной, но и расстоянием d от линии ее  действия до оси вращения, называемого плечом силы. Векторное  произведение  M =[rF] или M = r F sinα называют моментом силы, где r- радиус-вектор, проведенный из точки О, обозначающей  ось вращения, к точке приложения силы. Плечо силы d =r sin α, где α – угол,  между направлением силы  F и   радиус-вектора  r.

Разобьем мысленно тело на материальные точки массой m_i c  расстоянием  до оси вращения  r_i. Пусть под  действием   силы  F тело начало вращаться.  Это  значит,  что каждая точка   тела получила ускорение a_i ,  По второму закону  Ньютона  для каждой    точки тела можно записать F_i  =m_ia_i .  Умножим обе части равенства  на радиус вращения точки r_i

F_i r_i   =m_i a_i  r_i .

Учитывая, что a_i = r_i∙ε; M_i = F_ir_i , запишем M_i = m_ir_i² ε. Величина J_i = m_ir_i²   называется  моментом  инерции  материальной точки,  а сумма    моментом инерции тела относительно оси вращения. M_i= J_i∙ε. Суммируя последнее равенство по  всем точкам тела,  получим:

M= J ε    или    ε  = M/ J  -