Физика (Часть 1): Учебно-практическое пособие, страница 21

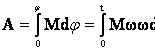
Если М=const, то A=M∙φ. Эта работа затрачивается на изменение кинетической энергии вращающегося тела

Основное уравнение  динамики  вращательного   движения.

При постоянном вращающем моменте  M=const  угловое ускорение  будет также постоянным ε =const  и вращение будет равно переменным. Поэтому, если начальная скорость вращения была ω₀ , а через промежуток времени Δt под действием момента  M внешних сил она стала ω, то угловое ускорение

и основное уравнение динамики вращательного движения  примет вид:

   или      M Δt = J ω  - J ω_0.

Произведение M Δt называют импульсом момента сил, Jω – моментом импульса тела. Это уравнение представляет собой выражение основного закона динамики вращательного движения: Импульс вращающего момента сил , действующих на тело, равен изменению момента импульса тела.

Момент импульса тела.  Закон сохранения момента импульса.

Импульсом тела при всяком движении, как известно, называют величину    р= mv. При изучении вращательного движения тела аналогично моменту силы вводят векторную величину L =[rp] =m [rv], называемую момента импульса. Выясним, чем определяется изменение моментом импульса L со временем. Для этого продифференцируем L по t

Если мы рассматриваем материальную точку, то ее расстояние от оси вращения остается неизменным  r = const.   Т.е.  dr/dt = 0,  а   следовательно,

Рассмотрим изменение момента импульса L c другой стороны, исходя  из уравнения вращательного движения: M = Jε,  ε = M/J. Если вращательный  момент M постоянен, то и угловое ускорение будет величиной постоянной и его можно выразить 

где Δt = t – t₀ ; ω₀ – начальная угловая скорость; ω – угловая скорость через промежуток времени Δt. Тогда уравнение    вращательного движения, можно записать в виде

   или   MΔt

Сравнивая это выражение с dL/dt = M, нетрудно убедиться, что  Jω  = L – есть  момент импульса. Импульс момента силы и момент импульса являются величинами векторными и совпадают по направлению с M и ω. При вращательном движении тела каждая его частица  движется с  линейной скоростью v_i = ω r_i , где r_i  -  радиус окружности, которую описывает  частица массой  m;   ω – угловая скорость,  одинаковая   для  всех  точек  тела. Момент импульса каждой  частицы  тела  равен  L_i =  m_i  r_i  v_i  = m_i  ω  = ωJ_i . Суммарный момент  импульса тела   будет   

ω ωJ,

или в векторном виде L = J ω.  Известно, что dL/dt = M, откуда dL =Mdt  . Рассматривая  это  выражение, можно отметить, что если  M = 0,  то, a следовательно,  L = const, т.е. J ω = const, если М = 0.

Эта формула является выражением закона сохранения  момента импульса  тел системы.   Если вектор  суммарного  момента внешних сил, действующих   на систему тел  относительно   неподвижной оси,  равен  нулю M = 0, то   векторная сумма моментов импульсов тел  системы не изменяется со временем, т.е.  остается   постоянной