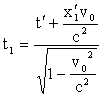Физика (Часть 1): Учебно-практическое пособие, страница 26

 ;                       ,

t₁  ≠   t_{2 ,}         так как          x'₁  ≠  x'₂ .

Относительность продолжительности событий. Эффект замедления времени.

Продолжительность событий в  классической механике  не зависит от выбора системы отсчета. Пусть в движущейся со скоростью v₀   системе отсчета K'   в неподвижной точке x'  произошло событие длительностью  Δt = t'₂ – t'₁ ,  где t'₁  и  t'₂ – моменты начала и конца события  (например,  включения и выключения  лампочки по  часам, покоящимся в системе  отсчета K' ).  Наблюдатель в неподвижной системе  K отметит по своим часам  (часам своей системы)  начало и  конец события в моменты t₁  и  t₂ ,  которые  будут связаны  с   моментами    t'₁  и     t'₂    соотношениями:

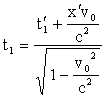
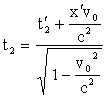
Отсюда длительность события Δt= t₂-t₁ в неподвижной системе отсчета K равна

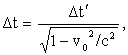
т.е. представляется более длительным, чем  в системе K′ (эффект замедления времени).

Относительность длины.   Пусть в движущейся  вдоль оси х' системе K'   покоится отрезок  длиной    Здесь x'₂  и x'₁  координаты начала и конца отрезка,  отмеченные  в  один и тот же момент времени t'.  Если измерение длины проведено в системе отсчета,  в  которой отрезок покоится, ее называют собственной длиной и обозначают  . Какова  будет длина  того же отрезка, если  ее измерить в неподвижной системе  отсчета K? Для  наблюдателя в системе отсчета K отрезок  будет двигаться со скоростью v_0.  Чтобы измерить длину движущегося отрезка, наблюдатель  в системе K должен в один  и тот же момент времени t  (по часам своей  системы) отметить на оси х положение  концов  движущегося отрезка.  Отметки эти нужно сделать именно в один и тот же момент времени, так как отрезок и его концы постоянно  смещаются  вдоль оси  х.

Пусть этими отметками будут координаты  х₁ и х₂ .  Но  координаты х₁ и х₂  связаны  с х'₁ и  х'₂  соотношением

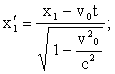
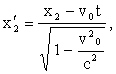         отсюда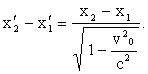  

Введя обозначения l  =  x₂  -x₁ ;   l₀ = x'₂ – x'₁ , получим

.

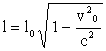Таким образом, наблюдатель в неподвижной системе K находит, что длина  движущегося отрезка  в 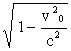          раз меньше его собственной длины, измеренной в системе , где этот отрезок покоится. Наблюдатель в  системе K обобщит этот  факт  следующим образом: в любой движущейся относительно него инерциальной системе отсчета , все  отрезки укорачиваются в направлении движения  системы  и  тем значительнее,   чем больше скорость, с какой движется эта система. Другие координаты  y и z  будут  неизменными.

Какой вывод можно сделать из  сказанного?

Относительность одновременности, длины предметов, продолжительности событий свидетельствуют о взаимосвязи пространства  и времени, о том,   что пространство и время зависят от движения  материальных объектов, с которыми связываются  инерциальные  системы отсчета. Чтобы это понять,  нужно отрешиться от привычных ньютоновских представлений об  абсолютности пространства  и времени.