Физика (Часть 1): Учебно-практическое пособие, страница 18

а) ;  б) ;  в) ;  г) ;  д) .

Пример решения задач.

Груз массой 700 кг падает с высоты 5м для забивки сваи массой 300кг. Найти среднюю силу сопротивления грунта, если в результате одного удара свая входит в грунт на глубину 4 см. Удар между грузом и сваей считать абсолютно неупругим.

              Дано: m₁=700кг; h=5м; m₂=300кг; s=4см=0.04м

              Найти: F_ср.

              Решение. По условию задачи удар неупругий, и поэтому груз и свая после удара двигаются вместе, их путь s=4см. На движущуюся систему действует сила тяжести и сила сопротивления грунта F_ср. По закону сохранения энергии

Т+П=А,   (1)

Где Т- кинетическая энергия; П- потенциальная энергия; А- работа сил сопротивления, которую можно определить по формуле А= F_срs. При движении системы на пути s изменяются её потенциальная и кинетическая энергия

П=(m₁+m₂)gs;

,

где u – общая скорость груза и сваи после удара (в начале их совместного движения). Используя это, запишем равенство (1) в виде

.        (2)

Для оценки средней силы сопротивления F_ср установим значение общей скорости и сваи, для чего применим закон сохранения импульса:

.         (3)

Для системы «груз - свая» закон сохранения импульса имеет вид:

,       (4)

где v – скорость груза в конце его падения с высоты h; m₁ν – импульс груза в конце его падения до удара о сваю;  - импульс груза и сваи после удара.

     Скорость груза v в конце падения с высоты h определяются без учета сопротивления воздуха и трения:

.                    (5)

Общая скорость груза и сваи после удара находится из формул (4) и (5):

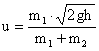              (6)

Определим среднюю силу сопротивления материала F_ср из формул (2)и (6):

F_ср  (7)

    (8)

. F_ср 

Глава 3. ОСНОВЫ КИНЕМАТИКИ  И  ДИНАМИКИ

ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

КИНЕМАТИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

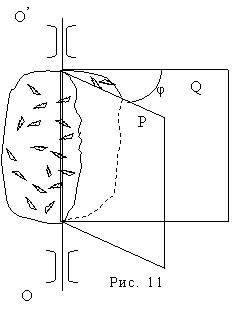Вращательным называется такое движение, при котором  все точки тела движутся в параллельных плоскостях  по  окружностям, центры  которых  лежат на одной прямой, называемой осью вращения. Рассмотрим абсолютно твердое тело с закрепленной осью вращения  OO΄. Проведем через ось две плоскости P и Q.  Неподвижная плоскость Q будет являться телом отсчета (аналогичной началу координат), а плоскость P, связанная с вращающимся телом,  будет характеризовать положение тела в каждый момент  времени величиной двугранного угла φ.

Изменение угла поворота φ со временем φ = φ (t) будет уравнением вращательного движения тела (аналогичного уравнению s = s(t) при   поступательном движении тела).

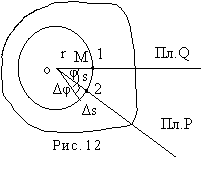При вращении всего твердого тела в целом  отдельные  его точки движутся по окружностям. Рассмотрим  движение точки M находящейся на расстоянии  r от оси вращения   (рис. 12).  Если тело повернулось на угол φ, то точка M перешла из положения 1 в положение 2 и прошла путь s, равный  s = r∙φ,где угол φ измерен в радианах .