Физика (Часть 1): Учебно-практическое пособие, страница 14

_срх

Из закона сохранения импульса вытекает, что центр инерции замкнутой системы тел либо остается неподвижным,   либо движется равномерно и прямолинейно.

Работа и мощность

Действие силы  F на   пути  s характеризуется  работой, которая является  количественной  мерой процесса обмена энергией между взаимодействующими телами. Энергия-это универсальная мера  различных форм  движения и взаимодействия материи (механическая,  тепловая, электромагнитная  ядерная и др.).

1

Под действием  силы  F тело проходит путь  s.  При этом сила  либо изменяет скорость   тела,  либо компенсирует действие  других сил, препятствующих    движению  (например,  силы  трения). Если  тело движется прямолинейно под действием постоянной силы, и направление силы   F  совпадает с направлением перемещения  s, то  работа А равна  скалярному произведению F и   s.

А=  F ·  s   =  F · s   [Дж =Н · м ].

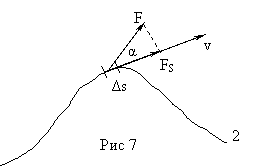Если сила F составляет с направлением  перемещения угол α (рис. 7),  то работа

A  =F_s · s  = F·s · cos α ,

где F_s=F·cosα - проекция силы на направление

перемещения. Работа - величина алгебраическая.

Если : 0 ≤ α < π / 2 , то cos α > 0 и А > 0;

        α  = π / 2, то cos α = 0 и А = 0;

        π / 2 < α ≤ π  , то  cos α < 0  и А < 0.

В  общем случае движение может быть  не прямолинейным и сила может изменяться по   величине и по направлению.

Для вычисления работы разобьем путь     на    элементарные участки  Δs  столь малые, что проекцию  силы F_s   на таком   участке можно считать  постоянной (рис.7).

Тогда работа  на каждом таком участке будет равна  ΔA_i  ≈  F_si  · Δs_i Работа на всем  пути s  будет  равна .                                  

При    Δs_i  →0  это приближенное равенство перейдет в строгое

   

      На графике  (рис.  8) полная работа  силы на  участке  1-2   равна  площади фигуры  1234.

 Скорость  совершения   работы характеризуется  мощностью:

  N =  dA/dt       [Вт],   1Вт= 1 Дж/c.

За  время  dt  сила  F  совершает   работу F_s ds  и  мощность, развиваемая этой силой в данный момент времени, равна        . Если направление действия силы совпадает с направлением  скорости , то  N=F ·v. В случае, если F  ≠ const,  то

Работа квазиупругой  или   упругой силы

Примером  работы, совершаемой   переменной  силой,  может  служить  работа упругой  силы. При  упругой   деформации, например,  при  сжатии или растяжении  пружины,  сила пропорциональна величине деформации x

F   =  ­­– kx ,

где k  – коэффициент упругости. Знак “минус” говорит о противоположном направлении силы и смещения x (деформация).

Элементарная работа  сжатия  равна  δА =  F dx      или    δА   =  -kx dx.

Определим работу  силы  F на пути  от x₁  до  x₂  . Для этого проинтегрируем последнее выражение