- во всех инерциальных системах отсчета одни и те же механические явления протекают одинаковым образом и никакими механическими опытами , проводимыми внутри данной механической системы отсчета, невозможно установить, покоится система отсчета или движется равномерно и прямолинейно.
В современной физике механика, как ее часть, подразделяется на три раздела: классическая, релятивистская и квантовая.
Классическая механика (механика Галилея-Ньютона) изучает законы движения макроскопических тел, скорости которых v малы по сравнению со скоростью света в вакууме c ( v « c ).
Релятивистская механика основана на специальной теории относительности
Эйнштейна и изучает движение макроскопических тел со скоростями, сравнимыми
со скоростью света.
Квантовая механика изучает движение микроскопических тел (атомы, элементарные частицы), значения физических величин которых квантуются, т.е. принимают дискретные значения.
Классическая механика базируется на абсолютности пространства и времени. Согласно воззрениям Ньютона пространство и время существуют сами по себе независимо друг от друга и независимо от других материальных тел. Абсолютность времени означает, что оно течет одинаковым образом во всех системах отсчета и для всех точек пространства – длительность одних и тех же процессов или событий во всех инерциальных системах отсчета одинакова; одно и то же событие во всех инерциальных системах происходит одновременно. Абсолютность пространства означает, что геометрические размеры тел остаются неизменными, в какой бы системе отсчета их не измеряли. Пространство и время не зависят от движения материальных объектов, с которыми связана система отсчета. Таким образом, в классической механике физические величины делятся на абсолютные (пространство, время, масса, геометрические размеры тел) и относительные (скорость, импульс, энергия и др.).
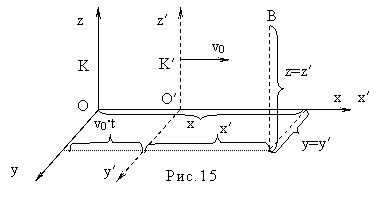
Преобразованиями Галилея называют преобразования (или связь) координат и времени в двух различных системах координат K и K' , когда одна система координат (K) считается неподвижной, а другая (K' ) движется относительно первой с постоянной скоростью. Рассмотрим две такие системы координат. Пусть система K покоится, а система K' перемещается относительно системы K вдоль оси x с постоянной скоростью v0. Чтобы убедиться в том, что математическая форма записи законов движения в рассматриваемых системах одна и та же, необходимо установить формулы перехода от координат x, y, z, t в системе K к координатам x' , y' , z' , t' в системе K' (рис. 15).
Связь координат точки B системах K и K' будет иметь вид:
x = x' + vo t x' = x- vo t
y = y' y' = y
z = z' z' = z
t = t' t' = t.
Допустим, что отсчет времени по часам той или другой системы начался с того момента времени, когда начала координат обеих систем совпадали. Если v0 « c, то часы обеих систем покажут одинаковое время, т.е. t'=t. Это соотношение выражает ньютоновскую концепцию абсолютности времени, одинакового для всех систем отсчета и точек пространства. Соотношение x'=x-vot отражает идею абсолютности пространства. Отрезок x', измеренный в системе K', определяется как разность двух отрезков ( x и vo t), замеренных в неподвижной системе отсчета K. Эти соотношения называются преобразованиями Галилея.
Преобразование скоростей не представляет труда. Если точка В движется в системе K с некоторой скоростью. то продифференцировав соотношения (x, y, z ) по времени, найдем связь между скоростями в точке В в системах K и K’:
vx = v'x + v0
v'x= vx - v0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.