1.3.3. Модели описания распределения плотности локализованных
состояний в щели подвижности
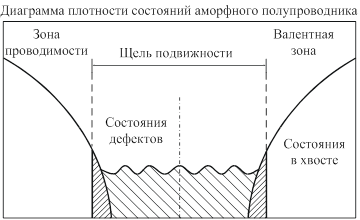
Рис. 3. Распределение плотности состояний в неупорядоченном полупроводнике на примере a-Si:H
Для описания распределения плотности состояний в щели подвижности аморфных полупроводников предложено несколько моделей, но в большинстве случаев они построены на общих принципах. Основа любой модели - наличие "хвостов" плотности состояний на краях валентной зоны и зоны проводимости, вызванных разупорядочением структуры аморфных полупроводников. Другая особенность аморфных полупроводников, отражаемая во всех моделях, - закрепление уровня Ферми вблизи середины щели подвижности (рис. 3).
Одной из первых появилась модель Коэна-Фрицше-Овшинского (КФО). В ней предполагается, что хвосты зон перекрываются в середине щели подвижности, образуя непрерывный спектр плотности состояний (рис. 4, а), уровень Ферми при этом закрепляется в области перекрытия хвостов. Состояния, возникающие из зоны проводимости, нейтральны, если они свободны (т.е. лежат выше EF ), а состояния, происходящие из валентной зоны, нейтральны, если заполнены. Другой принципиальной особенностью этой модели является понятие "краев подвижности", которые отождествляются с критическими энергиями, отделяющими локализованные состояния от распространенных. Дэвис и Мотт [19] высказали предположение, что появление перекрытия хвостов может возникать лишь при крупномасштабных флуктуациях плотности вещества и валентных углов, тогда как у идеального неупорядоченного полупроводника, примером которого могут служить стекла, в которых все связи насыщены и нет больших колебаний плотности, хвосты зон лежат неглубоко (рис. 4, б). Однако в реальных пленках всегда существуют дефекты структуры, такие как примеси, свободные связи, микропоры и т.д. Эти дефекты точно такие, как в кристалле, и могут приводить к появлению энергетических уровней внутри щели подвижности (рис. 4, в).
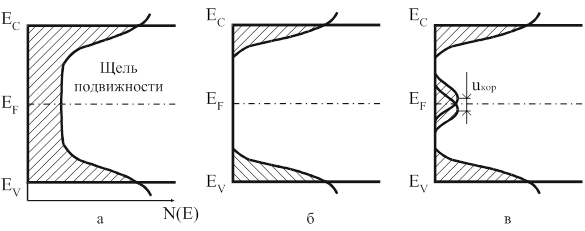
Рис. 4. Модели распределения плотности состояний для аморфных полупроводников: модель Коэна-Фрицше-Овшинского (а); модель идеального неупорядоченного полупроводника без структурных дефектов (б); уточненная модель Девиса-Мотта-Стрита (в). Локализованные состояния заштрихованы
Анализ экспериментальных данных по исследованию плотности локализованных состояний позволил нарисовать более явную картину распределения. Проявление прыжковой проводимости с переменной длиной прыжка вблизи уровня Ферми, сигнала электронного парамагнитного резонанса у пленок a-Si:H указывает на конечное значение плотности состояний. По результатам исследований методом эффекта поля оказалось, что минимум плотности состояний лежит между двумя максимумами [3].
На основании этих моделей и экспериментальных исследований для a-Si:Н удалось представить упрощенное распределение плотности состояний (рис. 5). Эксперименты по изменению дрейфовой подвижности и фотопроводимости подтверждают вид распределения, показанный на рис. 5. Вид обобщенного распределения схож с модельным распределением Коэна-Фрицще-Овшинского, однако, если в модели КФО речь идет о перекрытии хвостов зон, то в обобщенной модели имеется перекрытие распределения дефектов [24].
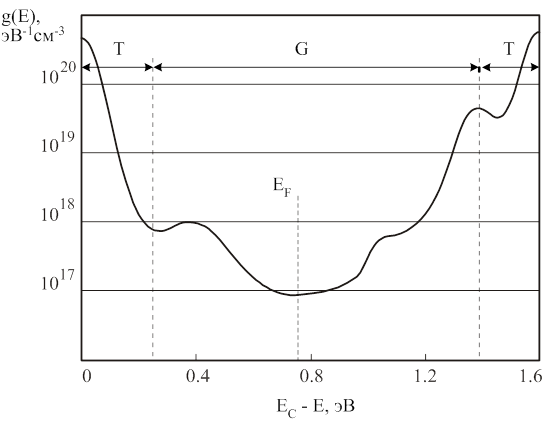
Рис. 5. Обобщенное распределение плотности состояний в щели подвижности a-Si:H [24]: G - состояния в щели подвижности, T- состояния в хвостах зон
В модели Девиса-Мотта-Стрита предполагается существование вблизи середины щели подвижности зоны локализованных состояний, которая и закрепляет там уровень Ферми [24].
Дальнейшее развитие моделей применительно к аморфному кремнию было сделано Д. Адлером в 1982 г. Наличие локализованных состояний в щели подвижности нарушает основные приближения теории твердого тела, которые не учитывают то обстоятельство, что два электрона могут коррелировать взаимные перемещения, чтобы свести к минимуму электростатическое отталкивание. Отталкивание между двумя электронами с противоположными спинами называется энергией корреляции (uкор). Величина этой энергии пренебрежимо мала для распространенных состояний, но для локализованных состояний может достигать десятых долей электрон-вольта. При этом считается, что состояния, лежащие ниже уровня Ферми, полностью заполнены, а лежащие выше уровня Ферми – пусты; расстояние между максимумами этих состояний по энергии равно uкор (рис. 4, в).
1.3.4. Заряженные дефектные состояния в неупорядоченных
полупроводниках
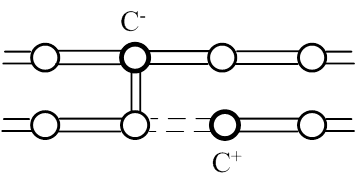
Многие из наблюдаемых оптических свойств неупорядоченных полупроводников можно объяснить изменениями зарядового состояния дефектов, создающих энергетические уровни в щели подвижности. Вследствие электрон-фононного взаимодействия оказывается энергетически выгодным электронное спаривание на дефектах, которые в нейтральном состоянии (D0) имеют орбитали, содержащие один электрон. Реакция 2D0 → D+ + D- является экзотермической. Здесь D+ - пустой дефект, a D- - дефект, содержащий два электрона. На примере халькогенидных стекол химическую природу этих состояний можно объяснить следующим образом. Халькоген с двойной координацией содержит четыре р-электрона, два из которых находятся на связывающих орбиталях, два других образуют отдельную пару. Следовательно, дефект D- образуется, когда одна связь разрушается и внешний электрон завершает образование второй отдельной пары. Возможно также, что образуется дефект D+, если два электрона удаляются из D-, оставляя пустую орбиталь отдельной пары. Изменение характера связи между D+ и D- происходит с выделением энергии. Это обусловлено электрон-фононным взаимодействием, которое преодолевает энергию электронного отталкивания в D- и делает энергетически выгодным спаривание электронов. Конфигурации связей этих двух состояний показаны на рис. 6 (дефекты в халькогенидных стеклообразных полупроводниках принято обозначать символом С (от chalcogen)). Число взятых вместе связывающих электронов и электронов отдельных пар такое же, как и в идеальной структуре, потому энергия образования пары D+ и D- мала по сравнению с энергией разрушения связи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.