Физические процессы в барьерных структурах на основе неупорядоченных полупроводников: Учебное пособие, страница 18

Из описанной модели формирования барьера можно сформулировать следующие выводы:

- увеличение плотности состояний в середине щели подвижности приводит к сужению ОПЗ и изменению j(х), утоньшению барьера в приконтактной области и, как следствие, понижению эффективной высоты барьера, изменению суперпозиции токов, протекающих через барьер;

- барьер формируется за время t_S » t_M ≤ 10^-3 с, т.е. для измерения вольтфарадных характеристик частота тест сигнала должна быть соизмерима или меньше t_M^-1;

- на контакте Me-a-Si:H формируется барьер типа Шоттки, хотя классическая теория барьеров Шоттки не допускает формирования слоя Шоттки в собственном полупроводнике.

Таким образом, данная модель может быть применима для описания формирования барьера между металлом и некристаллическим полупроводником, имеющим высокую плотность глубоких состояний и низкую подвижность носителей.

2.3.2. Решение уравнения Пуассона для неупорядоченного полупроводника

Для получения распределения пространственного заряда r(x), профиля электростатического потенциала j(x) и напряженности электрического поля F(x)  в ОПЗ на контакте Me/a-Si:H решается уравнение Пуассона с учетом особенностей электронного строения и электрофизических свойств a-Si:H.

Уравнение Пуассона устанавливает взаимосвязь между плотностью объемного заряда r(x) и ходом электростатического потенциала r(x) в ОПЗ полупроводника:

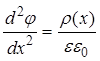,                                             (69)

где для простоты в промежуточных расчетах координата x отсчитывается от внутренней границы ОПЗ.

Для его решения сформулируем следующие граничные условия:

1 ^*. Расстояние в запирающем слое на границе Me/a-Si:H отсчитывается от поверхности в глубь полупроводника (рис. 24), однако в промежуточных расчетах для простоты координата отсчитывается от внутренней границы ОПЗ [39].

2 ^*. Функция Ферми для электронов имеет вид [33]:

,

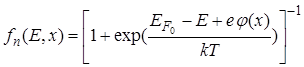где E_F0 – глубина залегания уровня Ферми в объеме a-Si:H; ej(x) – изгиб зоны на расстоянии x от границы Me/a-Si:H; kT – тепловая энергия, эВ.

3 ^*. При отсутствии внешнего электрического поля на внутренней границе ОПЗ значения электростатического потенциала j и внутреннего электрического поля F равны нулю; на границе Me/a-Si:H – j₀ и F₀ соответственно.

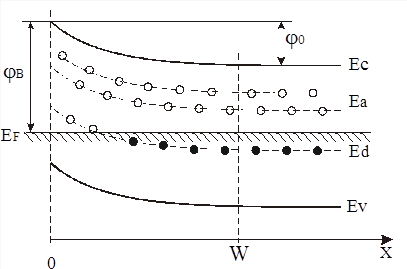
Рис. 24.  Зонная диаграмма контакта Me/a-Si:H. j₀ – изгиб зон в ОПЗ полупроводника,        W – толщина ОПЗ

В зависимости от расстояния в запирающем слое r(x) определяется разностью подвижного (электронов) и неподвижного (ионизированных донороподобных состояний, локализованных в щели подвижности) зарядов:

,                                      (70)

или - в зависимости от электростатического потенциала:

,                                      (71)

где e – заряд электрона, N_d⁺(x) или N_d⁺(j) – концентрация ионизированных донороподобных состояний в зависимости от расстояния или электростатического потенциала в запирающем слое, n(x) или n(j) – концентрация электронов.

Для определения N_d⁺(j) используются модель Коэна-Фрицше-Овшинского распределения плотности состояний (ПС) в щели подвижности a-Si:H и экспоненциальная аппроксимация распределения ПС (рис. 4, а):

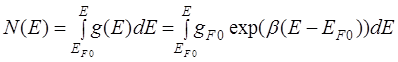,           (72)

где g_F0 – плотность состояний вблизи уровня Ферми, b - параметр аппроксимации распределения ПС. Переходим в формуле (72) от интегрирования по энергии к интегрированию по потенциалу:

.                        (73)

Тогда формулу (72) с учетом (73) переписываем в следующем виде:

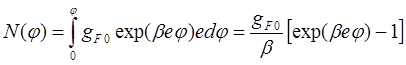.             (74)

Концентрация свободных электронов в ОПЗ:

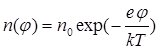.                                     (75)

Тогда формулу (71) с учетом (74) и (75) можно записать следующим образом:

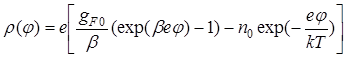.                    (76)

Рассмотрим область пространственного заряда при сильном изгибе зон, т.е. считаем, что ej >> kT. При этом exp(bej) >> 1; exp(-ej/kT) ® 0. При таком допущении уравнение (76) переписываем в следующем виде:

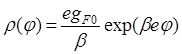.                                    (77)

Тогда уравнение Пуассона (69) можно записать так:

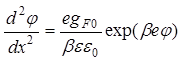.                                   (78)

Данное дифференциальное уравнение решаем методом разделения переменных с учетом граничных условий (1^*, 3^*). Зависимость электростатического потенциала от расстояния в ОПЗ выражается следующей формулой:

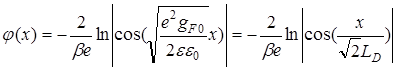,                (79)

где длина экранирования L_D, в отличие от кристаллов (27), определяется иначе [40]:

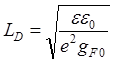.                                         (80)

Полученные результаты значительно отличаются от данных, полученных для кристаллических полупроводников (20), а также от аналогичных расчетов, полученных в работах В.В. Ильченко и В.И. Стрихи [41]. Данные результаты отличаются более высокой точностью. Во-первых, "опорной точкой" аппроксимации плотности электрически активных состояний является ее значение на уровне Ферми, а не на хвостах зон, как в [41]. Во-вторых, в выражении (79) переменные носят однозначный физический смысл и характеризуют свойства материала. И, в-третьих, теоретически рассчитанные зависимости находятся в хорошем согласии с экспериментальными данными (рис. 25 и 26) и удачно вписываются в теорию формирования барьеров на неупорядоченных полупроводниках [24].

Анализ (79) показывает, что ход потенциала в ОПЗ определяется значением ПС вблизи уровня Ферми g_F0 и параметром аппроксимации b, характеризующим распределение ПС в щели подвижности [42]. Рассчитанный ход потенциала оказывается более "крутым" по сравнению с кристаллическим барьером (рис. 26), т.е  распределение электрического поля F(x) = dj/dx отличается от линейного закона и достигает больших абсолютных значений [43]:

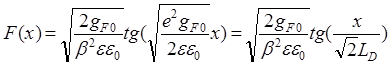.                (81)

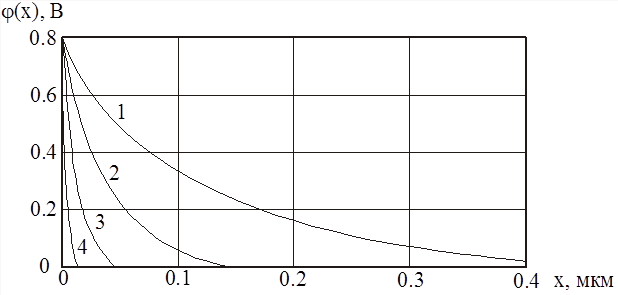
Рис. 25. Ход электростатического потенциала в ОПЗ в зависимости от параметров полупроводника:   1 – g_F0 = 10¹⁶ см^-3эВ^-1, b = 5.76 эВ^-1, W = 0.52 мкм; 2 – g_F0 = 10¹⁷ см^-3эВ^-1, b = 5.18 эВ^-1, W = 0164 мкм;   3 – g_F0 = 10¹⁸ см^-3эВ^-1, b = 4.32 эВ^-1, W = 0.049 мкм; 4 – g_F0 = 10¹⁹ см^-3эВ^-1, b = 2.88 эВ^-1, W = 00.14 мкм

Если известна высота потенциального барьера j₀ на границе Me/a-Si:H, то можно рассчитать толщину ОПЗ при отсутствии внешнего смещения [39]:

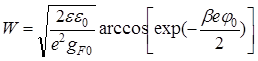.                           (82)