Форма потенциального барьера зависит от распределения заряда в приконтактной области, обедненной свободными носителями заряда (области пространственного заряда – ОПЗ). Если дно зоны проводимости поднимается примерно на 3kТ выше его положения в объеме полупроводника, то концентрация электронов уменьшается на порядок и пространственный заряд в ОПЗ практически полностью равен положительному заряду на ионизированных донорах. Если пренебречь изгибом зон в переходной области, где концентрация электронов меньше концентрации доноров, а разность концентраций не превышает одного порядка (так называемое приближение полного обеднения), то форма барьера будет определяться только распределением доноров по координате [28].
Рассмотрим зависимость напряженности поля и электростатического потенциала от расстояния в ОПЗ и концентрации доноров в объеме полупроводника. Взаимосвязь между потенциалом в ОПЗ j и плотностью объемного заряда r(x) устанавливается уравнением Пуассона:
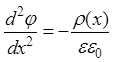. (16)
В приближении полного обеднения можно считать, что заряд ОПЗ определяется только ионизированными донорами, электронами в этом случае можно пренебречь. Тогда
, (17)
где Nd+ - концентрация доноров, n0 – концентрация свободных электронов в объеме полупроводника. Таким образом r(x) можно полагать постоянным во всем слое ОПЗ, а уравнение (16) переписать следующим образом:
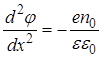. (18)
Для решения этого дифференциального уравнения необходимо сформулировать граничные условия. На внутренней границе ОПЗ при x = W (координата отсчитывается от границы раздела вглубь полупроводника) напряженность контактного поля F(W) = 0 и потенциал j(W) = 0. Решение уравнения (18) с учетом граничных условий дает следующие результаты для распределения поля и потенциала в ОПЗ:
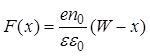; (19)
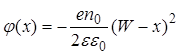. (20)
Здесь W – ширина слоя ОПЗ; e0 = 8.85´10-14 Ф/см; e - относительная диэлектрическая проницаемость (для кремния – 11,7).
Напряженность поля является линейной функцией x, как это показано на рис. 11, в. Поле направленно к металлу, максимальное значение поля достигается на границе раздела с металлом:
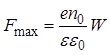. (21)
Потенциал имеет квадратичную зависимость от координаты, знак минус в формуле (20) указывает на характер изменения потенциала. Максимальное абсолютное значение потенциал имеет на границе раздела:
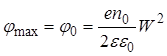. (22)
Следует отметить, что условие постоянства объемного заряда (17) является приближенным, особенно для внутренней области обедненного слоя. В этом случае нельзя не учитывать вклад электронов в общий заряд ОПЗ:
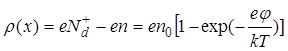. (23)
Если изгиб зон небольшой (ej << kT), то экспоненту можно разложить в ряд:
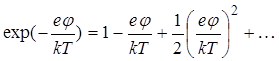. (24)
Ограничиваясь двумя первыми членами ряда, получаем:
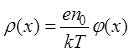. (25)
Тогда уравнение Пуассона будет иметь следующий вид:
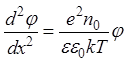. (26)
Если обозначить
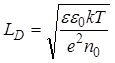, (27)
т.е. ввести дебаевскую длину экранирования, то получим:
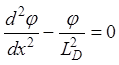. (28)
Для решения этого дифференциального уравнения необходимо задаться граничными условиями. В толще полупроводника j = 0, а при x = 0 j = j0. Здесь j0 – абсолютная величина потенциала при условии ej << kT, т.е в так называемой квазинейтральной области. Решение уравнения (28) с учетом граничных условий дает экспоненциальную зависимость потенциала от координаты для квазинейтрального слоя:
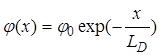. (29)
Таким образом, дебаевская длина экранирования LD представляет собой глубину проникновения поля в квазинейтральной области, на котором потенциал по абсолютному значению уменьшается в e раз [11].
Все изложенное можно применить к запирающему слою, как находящемуся в равновесии, так и при наложении внешнего постоянного поля. В общем случае падение напряжения на контакте
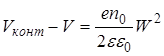, (30)
где Vконт – контактная разность потенциалов, V – внешнее напряжение. В частном случае, когда V = 0, Vконт = j0 (ej0 – высота потенциального барьера со стороны полупроводника при отсутствии внешнего поля, j0 также называют "встроенным диффузионным потенциалом").
В случае, когда к контакту приложено внешнее постоянное поле, оно распределится полностью в полупроводнике, т.к. падение напряжения на объемном заряде в металле практически равно нулю. Здесь предполагается, что металл является идеальным проводником и заряды, перешедшие в него из полупроводника, располагаются в тонком слое его поверхности. Равновесная зонная диаграмма изменится, как показано на рис. 13. При этом изменится искривление зон, а это значит, что падение напряжения будет отличаться от j0 (30).
Таким образом, свободные электроны в объеме полупроводника удерживаются от перехода в металл барьером, высота которого равна qj0 при термодинамическом равновесии. При приложении внешнего смещения высота барьера изменяется: уменьшается, если металл находится под положительным смещением относительно полупроводника, и увеличивается, если смещение имеет противоположную полярность. Энергетические зонные диаграммы для этих двух случаев изображены на рис. 13. Эти диаграммы соответствуют неравновесным условиям, поэтому уровень Ферми для них не сохраняется везде постоянным. Энергия Ферми в области, из которой вытекают электроны, выше энергии Ферми в области, куда втекают электроны. Направление токов, как всегда, принято противоположным направлению электронов.
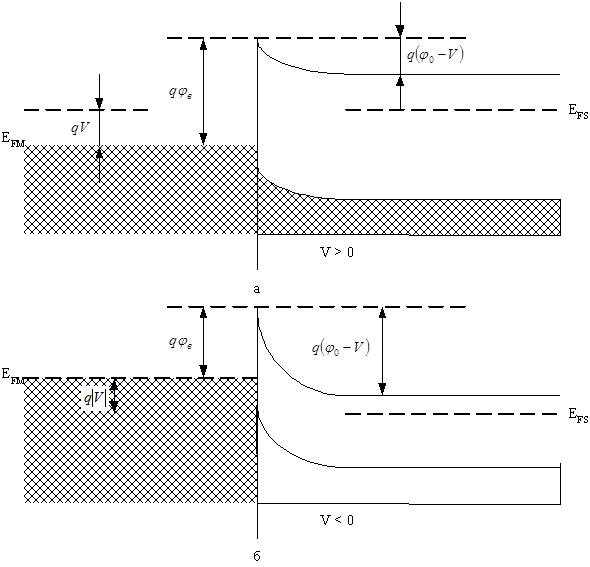
Рис. 13. Идеализированная зонная диаграмма для перехода металл-полупроводник: а – при смещении в прямом направлении; б – при смещении в обратном направлении
Из уравнения (30) можно выразить ширину ОПЗ:
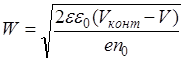. (31)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.