где
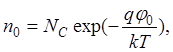 (47)
(47)
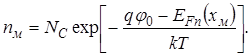 (48)
(48)
Решение уравнения (46) в соответствии с граничными условиями имеет следующий вид:
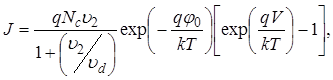 (49)
(49)
где ud – эффективная скорость дрейфа и диффузии электронов вблизи (j b):
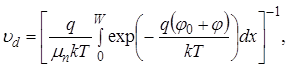 (50)
(50)
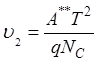 . (51)
. (51)
Здесь А** – постоянная Ричардсона. Для Si, Ge и GaAs n – типа u2 равно соответственно 7´106; 5,2´106; 107 см/с.
При условии ud >> u2 уравнение (49) принимает вид (39), т.е. применима диодная теория.
При условии ud << u2 уравнение (49) преобразуется в (42), т.е. вступает в силу диффузионная теория.
Физическая картина этого условия выглядит следующим образом. Электроны, проходящие над барьером в металл, имеют в среднем последнее столкновение на расстоянии длины свободного пробега от максимума барьера. Если d << 1, где d – расстояние, на котором барьер уменьшается на kT (d = kT/Fmax), то незначительная часть электронов имеет энергию, достаточную для преодоления барьера, и они не могут существенно изменить концентрацию электронов при x = l. Следовательно, электроны в целом остаются в термодинамическом равновесии с электронами в объеме полупроводника вплоть до расстояния l от границы раздела, что и предполагается в диодной теории Бете. Однако, если d >> 1, то почти все электроны смогут преодолеть барьер, и поток электронов в металл будет приводить к существенному уменьшению концентрации электронов в объеме полупроводника, что согласуется с диффузионной теорией Шоттки [29].
2.2.5. Теория полевой и термополевой эмиссии
Анализ ВАХ контакта металл-полупроводник с высокой концентрацией примеси в полупроводнике показывает, что они не подчиняются рассмотренным теориям. Для сильнолегированных полупроводников слой ОПЗ очень тонок, и поэтому преобладающим механизмом токопереноса будет туннелирование носителей заряда. Энергетическая диаграмма контакта в этом случае представлена на рис. 17. В области низких температур преобладает полевая эмиссия (туннелирование), в области средних температур – термополевая эмиссия (термоэлектронная эмиссия и туннелирование), а в области высоких температур – уже известная термоэлектронная эмиссия.
Для низких температур прямая ВАХ имеет вид:
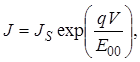 (52)
(52)
где 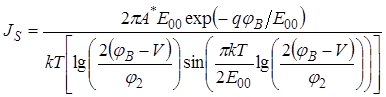 , (53)
, (53)
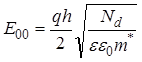 .
(54)
.
(54)
Здесь h – постоянная Планка; m* – эффективная масса электрона; Nd – концентрация доноров; j2 – потенциал уровня Ферми полупроводника по отношению к дну зоны проводимости. Если построить ВАХ в полулогарифмическом масштабе, то получится прямая линия, наклон которой равен q/E00.
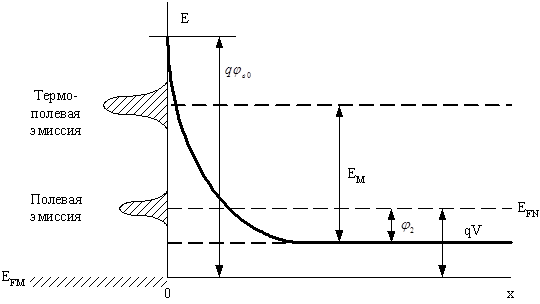
Рис. 17. Энергетическая диаграмма контакта металл-полупроводник при прямом смещении для полевой и термополевой эмиссии
Для средних температур в предположении, что большинство электронов туннелируют при E = EM, ВАХ имеет вид:
![]() (55)
(55)
где 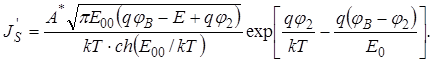 (56)
(56)
![]() .
(57)
.
(57)
В этом случае наклон ВАХ в полулогарифмическом масштабе равен q/E0. Аналогично записываются ВАХ для обратного смещения [29, 31].
Отношение kT/E00 является критерием того, с чем связано токопрохождение. В первом приближении можно считать, что полевая эмиссия преобладает, если kT << E00, термополевая – если kT ≈ qE00, и термоэмиссия – при kT >> E00. Более точные выражения для критерия вида эмиссии даны в работе [29].
Необходимо также заметить, что энергия E00 имеет физический смысл диффузионного потенциала барьера Шоттки, при котором вероятность туннельного происхождения электрона с энергией, соответствующей дну зоны проводимости на краю обедненной области, равна exp -1.
2.2.6. Постоянная Ричардсона
Величина А* (постоянная Ричардсона) является одной из важнейших постоянных в теории контакта металл-полупроводник с барьером Шоттки. Для термоэлектронной эмиссии в вакуум постоянная Ричардсона А* = 120 А/(см2´К2). В табл. 1 и 2 представлены численные значения отношений А*/А для термоэлектронной (табл. 1) и термополевой (табл. 2) эмиссий. Отношение А*/А и m*/m0 в значительной степени зависит от полупроводника и типа его проводимости (m0 – масса покоя свободного электрона).
Во многих случаях сохраняется вероятность электронно-оптического отражения электронов от барьера, даже если он обладает энергией, достаточной для преодоления этого барьера [29]. Кроме того, после прохождения барьера электрон может претерпевать рассеяние с поглощением или испусканием фотона и возвращаться обратно. Последний процесс наиболее вероятен на участке от 0 до хм (рис. 17). Кроуэлл и Зи предложили описывать вероятность перехода электронов через барьер функцией fp, а квантовомеханический коэффициент передачи – функцией fq. С учетом сделанных замечаний постоянную Ричардсона можно записать следующим образом:
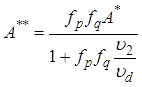 .
(58)
.
(58)
Таблица 1
Значения А*/А при термоэлектронной эмиссии
|
Полупроводник |
Тип проводимости |
||
|
p |
n <111> |
n <110> |
|
|
Ge Si GaAs |
0,34 0,66 0,62 |
1,11 2,2 0,068 (сильное поле) 1,2 (слабое поле) |
1,19 2,1 0,068 (сильное поле) 1,2 (слабое поле) |
Таблица 2
Значения А*/А при термополевой эмиссии
|
Полупроводник |
Ориентация |
m*/m0 |
А*/А |
|
Si Si Ge Ge |
<111> <110> <111> <100> |
0,259 0,1905 0,096 0,12 |
0,358 0,415 0,329 0,238 |
Для Si при комнатной температуре и напряженности поля F = 4×106 В/м при Nd = 1022 м -3 коэффициент fp = 0,95. Для GaAs fp = 0,85 вследствие большего взаимодействия электронов с фононами в полярных полупроводниках. Величина fp асимптотически приближается к 1 при увеличении Fmax и уменьшается с температурой вследствие увеличения числа фононов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.