где Nd – концентрация ионизированных доноров.
Кроме ограничений по вертикальному размеру структуры металл-полупроводник, существуют критерии минимальной площади структуры, одним из которых является критерий сохранения плоской конфигурации ОПЗ. В этом случае для структуры квадратной формы со стороной d должно выполняться условие d >> W. Однако выпрямление в структуре сохраняется и при d << W.
Существует ряд физических ограничений размеров структуры d. Они связаны с тем, что в малых объемах и при малых площадях имеет место флуктуация количества ионизированных примесей и поверхностных состояний. Поэтому при уменьшении размеров структуры наблюдается флуктуация параметров, определяющих ВАХ, ВФХ, и становится невозможным создание элементов с воспроизводимыми характеристиками.
На рис. 28 представлены результаты исследования влияния перехода к субмикронным размерам структур Al/n-Si на высоту барьера.
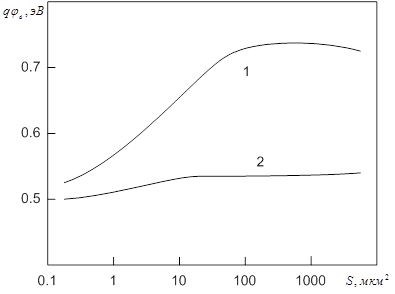
Рис. 28. Зависимость высоты барьера Шоттки от площади структуры Al/n-Si: 1 – без отжига; 2 – отжиг при 500 °С
Как видно, при S > 10 мкм2 jB слабо зависит от изменения площади контакта для отожженного образца и практически не зависит для неотожженного.
Таким образом, с учетом рассмотренных ограничений минимальные размеры d структур Шоттки для кристаллического кремния изменяются в пределах 0,06 … 0,3 мкм, а изменения электрофизических характеристик при переходе к субмикронным размерам связаны с нарушением плоскостной формы ОПЗ вдоль периметра структуры.
2.4.2. Эффект Шоттки
При обратном включении барьера Шоттки существует небольшая зависимость высоты барьера от величины приложенного напряжения. Эта зависимость впервые была объяснена Вальтером Шоттки при изучении эмиссии электронов в вакуум.
Для анализа этого явления рассмотрим контакт металл – кристаллический полупроводник n-типа, при этом используем следующие допущения:
1) металл будем рассматривать как плоский проводящий слой;
2) электрон будем считать свободным, обладающим эффективной массой mn*. Это позволяет описать движение электрона в периодическом потенциальном поле кристаллической решетки полупроводника как движение свободной частицы.
Поле к полупроводнику прикладывается таким образом, чтобы удалить электроны от поверхности металла.
Функция Е1(х), представляющая на рис. 29 энергию электрона, рассчитана классическими методами: свободный электрон, находящийся на некотором расстоянии от металла, индуцирует в металле положительный заряд, расположенный симметрично относительно плоскости x = 0. В присутствии поля F, стремящегося удалить электроны от поверхности металла, энергия электрона равна сумме:
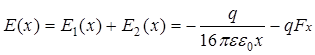 .
(95)
.
(95)
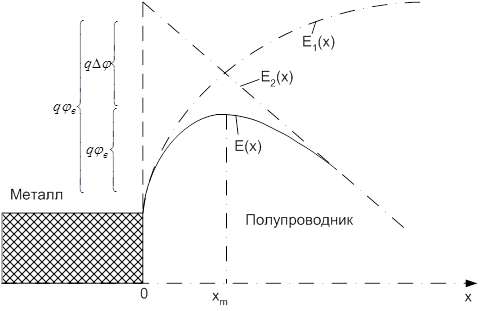
Рис. 29. Энергетическая диаграмма для свободного электрона вблизи плоской металлической поверхности: Е1(х) – при тепловом равновесии, Е(х) – для случая приложенного поля
Уравнение (95) может считаться точным для расстояний, больших нескольких нанометров. Плоскость, в которой Е(х) максимальна, может быть найдена так же, как и энергия qDj на рис. 29:
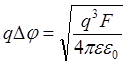 .
(96)
.
(96)
В соответствии с данной моделью высота барьера qjВ, препятствующего потоку электронов из металла, изменяется таким же образом, как и для qj0 . Ток зависит от этой высоты экспоненциально, так как через барьер может пройти из металла только та часть электронов, которая имеет энергию выше, чем максимальная высота барьера (энергии электронов распределены по закону Больцмана). Поэтому следует ожидать, что ток, эмитируемый из металла при обратном смещении, изменяется следующим образом:
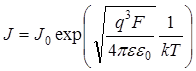 .
(97)
.
(97)
Используя приближение обеднения, можно связать поле F со смещением V и встроенным диффузионным потенциалом j0 с помощью следующего соотношения [29]:
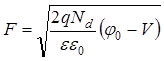 .
(98)
.
(98)
Следует отметить, что эффект Шоттки сказывается и на свойствах контакта металл – неупорядоченный полупроводник. Силы изображения оказывают существенное влияние на ход j(х) в ОПЗ в a-Si:H на небольшом расстоянии от границы раздела (~ 3 нм), где заряд в ОПЗ формируется за счет глубоких уровней в щели подвижности [30, 37]. Время, необходимое для перезарядки этих состояний, велико, оно может достигать значений порядка 103 с. Это означает, что при прохождении свободных носителей над барьером (jB) система связанных на локализованных состояниях зарядов не успевает следить за электронной подсистемой свободных носителей. Поэтому силы изображения не приводят к искажению j(х) в отсутствие свободных носителей.
Влияние сил изображения на j(х) усиливается с ростом разности j0 – eV при обратном напряжении. При увеличении напряжения в прямом направлении роль сил изображения уменьшается. Это происходит вследствие уменьшения напряженности электрического поля в области х = 0. Однако при этом должен увеличиваться изгиб квазиуровня Ферми. Расчет показывает [24], что изгиб уровня Ферми в ОПЗ при небольших положительных напряжениях усиливает влияние сил изображения на ход потенциала j(х), в то время как при больших изгибах зон влияние сил изображения за счет этого эффекта должно ослабляться.
Изменение профиля барьера за счет сил изображения оказывает влияние на ВАХ. Анализ зависимости наклона ВАХ от прикладываемого напряжения показывает, что с увеличением плотности локализованных состояний усиливается влияние сил изображения, которое проявляется в уменьшении коэффициента выпрямления диодной структуры. Основной вклад в это вносит увеличение тока насыщения структуры, который при больших изгибах зон (~ 0,9 эВ) возрастает на порядок.
ЗАКЛЮЧЕНИЕ
Контакт металл-полупроводник, будь то кристаллический или аморфный полупроводник, до сих пор является объектом исследования как ученых-теоретиков, так и инженеров-практиков. Особенно это касается контакта металла с аморфным полупроводником, где существуют проблемы теоретического плана – отсутствие единой барьерной теории, и практического – невозможность с достаточной точностью предсказывать параметры барьера и сложность в получении хороших омических контактов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.