При прямом включении, т.е. при V > 0, ширина слоя уменьшается с ростом V. Следует заметить, что при прямом включении запирающий слой существует лишь пока V < Vконт. При обратном включении, т.е. при V < 0, толщина слоя увеличивается с ростом абсолютного значения V.
Обедненный слой, способный изменять свою толщину по формуле (31), называется физическим запирающим слоем или барьером Шоттки. С увеличением n0 толщина слоя уменьшается, и наоборот, чем слабее легирован полупроводник, тем больше W.
Приведенное выше описание относится к полупроводнику n-типа с работой выхода qjS , которая меньше, чем работа выхода из металла qjM. Если рассмотреть случай, когда qjS > qjM , то получим зонную диаграмму, изображенную на рис. 14, б. Если к такому контакту приложить напряжение смещения так, чтобы электроны переходили из полупроводника в металл, то для них барьер будет отсутствовать. Если смещение таково, что электроны двигаются в обратном направлении, то область с относительно высокой концентрацией электронов, где зоны полупроводника загнуты вниз (обычно она называется обогащенной областью), ведет себя подобно катоду, который способен легко обеспечить большой поток электронов. В этом случае ток определяется сопротивлением объема полупроводника. Такой контакт ведет себя подобно омическому контакту. Падение напряжения на таких контактах пренебрежительно мало по сравнению с падением напряжения в объеме полупроводника. В результате в контактах не происходит выделения мощности, и омический контакт может рассматриваться как находящийся в тепловом равновесии. Это означает, что концентрации свободных носителей у омического контакта не изменяются при протекании тока.
Для полупроводника p-типа, в котором ejM > ejS , энергетическая диаграмма контакта имеет вид, приведенный на рис. 14, в. Такой контакт ведет себя также подобно омическому контакту. На рис. 14, г показан случай для полупроводника p-типа, когда ejS > ejM. Дыркам трудно проходить под барьером, поэтому контакт также обладает выпрямляющими свойствами и аналогичен контакту на рис. 14, а, но только для полупроводника p-типа.
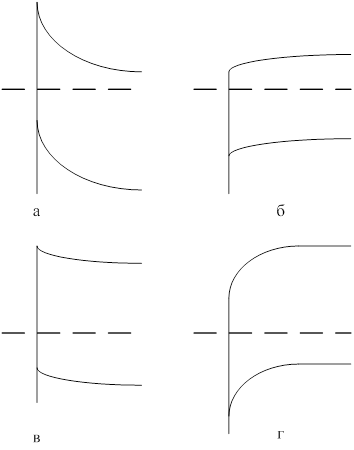
Рис. 14. Барьеры разных типов с разными работами выхода: n-тип: а – jM > jS – контакт выпрямляющий, б – jM < jS – контакт омический; p-тип: в – jM > jS – контакт омический, г – jM < jS – контакт выпрямляющий
2.2.2. Механизмы переноса заряда через барьер
На рис. 15 показаны четыре основных транспортных процесса при прямом смещении контакта Шоттки (при обратном смещении происходят обратные процессы). На рисунке показано понижение эффективной высоты барьера, особенно заметное при обратном включении. Этот эффект определяется действием сил зеркального изображения. Он получил название "эффекта Шоттки" и будет рассмотрен позднее.
Перечислим основные механизмы токопереноса:
1) надбарьерный перенос - преобладает в диодах Шоттки на умеренно легированных полупроводниках (в случае Si при температурах около 300 К Nd ≤ 1017 см-3); 2) квантомеханическое туннелирование электронов через барьер – наблюдается при высоких уровнях легирования, например, в туннельных омических контактах [9]; 3) рекомбинация в области пространственного заряда; 4) инжекция дырок из металла в полупроводник - процесс, аналогичный рекомбинации в нейтральном объеме. Кроме того, вклад в полный ток через диод Шоттки могут давать ловушки вблизи границы раздела металл-полупроводник и токи утечки в периферийных областях контакта, обусловленные высокой краевой напряженностью электрического поля. Для уменьшения тока через ловушки используют различные методы улучшения качества поверхности.
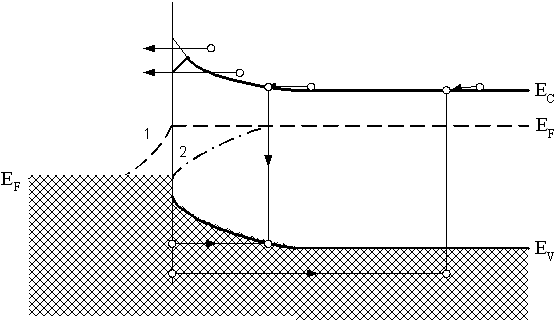
Рис. 15. Четыре основных процесса переноса при прямом смещении. Поведение квазиуровня Ферми для электронов в барьере Шоттки при прямом смещении: 1 – соответствует диодной теории; 2 – соответствует диффузионной теории
Рассмотрим надбарьерный перенос. Его можно разделить на два этапа. Во-первых, прохождение электронов из объема полупроводника к его поверхности. При этом при прохождении через ОПЗ полупроводника движение электронов подчиняется обычным процессам диффузии и дрейфа в электрическом поле барьера. Во-вторых, после достижения границы раздела происходит эмиссия электронов в металл. Оба процесса прохождения действуют последовательно, и ток через контакт определяется преимущественно тем процессом, которому полупроводник оказывает большое сопротивление. По диффузионной теории Вагнера, Шоттки и Шпенке именно первый процесс является ограничивающим, по диодной теории Бете – второй.
2.2.3. Диодная и диффузионная теории выпрямления на контакте Шоттки в кристаллических полупроводниках
Теорию выпрямления в тонком запирающем слое называют диодной, и обычно связывают с именем Х. Бете. Тонким запирающим (барьерным) слоем называют слой, ширина которого не превосходит длины свободного пробега носителей заряда. Плотность тока через запирающий слой рассматривают как плотность тока термоэлектронной эмиссии.
В диодной теории термоэлектронной эмиссии используются следующие положения:
- высота барьера много больше kT;
- область, определяющая термоэлектронную эмиссию, находится в термодинамическом равновесии;
- протекание полного тока не нарушает этого равновесия;
- не принимается в учет действие сил изображения.
Данные предположения позволяют считать, что полный ток через барьер представляет собой разность между током из металла в полупроводник и противоположным ему током из полупроводника в металл, причем металл и полупроводник характеризуются каждый своим квазиуровнем Ферми[1].
При использовании стандартного уравнения для термоэлектронной эмиссии в вакуум было получено выражение для плотности тока из полупроводника в металл (JS-M):
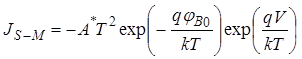, (32)
где А* – постоянная Ричардсона:
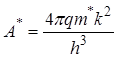. (33)
Здесь Т – температура; jB0 – высота барьера без учета понижения за счет действия сил изображения (рис. 9); m* – эффективная масса электрона; k – постоянная Больцмана; h – постоянная Планка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.