С учетом внешнего электрического смещения толщина ОПЗ в зависимости от высоты потенциального барьера определяется по (83):
,
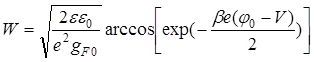(83)
где V – напряжение внешнего электрического поля. Причем, в формулах (82, 83) определяется толщина ОПЗ без учета квазинейтральной области, которая составляет 2 – 3 мкм для случая нелегированного a-Si:H (рис. 27).
Формулы (79 – 83) описывают профиль барьера на границе Me/a-Si:H в зависимости только от параметров полупроводника. Однако на практике характеристики барьера определяются также параметрами контактирующего металла и наличием внешнего электрического смещения.
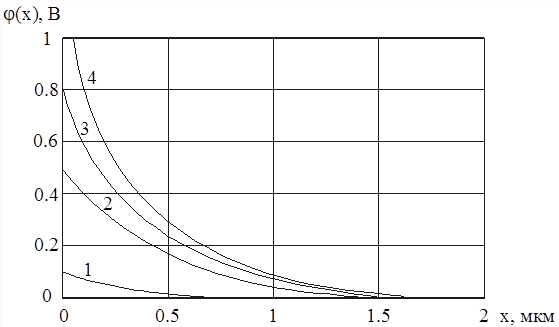
Рис. 26. Ход электростатического потенциала в ОПЗ в зависимости от внешнего напряжения. Параметры аппроксимации распределения ПС в щели подвижности: gF0 = 1016 см-3эВ-1, b = 5,76 эВ-1; j0 = 0,8 В. Внешнее смещение V и толщина ОПЗ W: 1 – V = 0,7 В, W = 0,085 мкм; 2 - V = 0,3 В, W = 0,158 мкм; 3 - V = 0 В, W = 0,174 мкм; 4 - V = - 0,5 В, W = 0,183 мкм
При экспериментальном исследовании барьерных структур удобнее отсчитывать координату от поверхности в глубь полупроводника, поскольку ширина ОПЗ точно не известна. Зная параметры контактирующих материалов (работа выхода, концентрация и подвижность носителей заряда, распределение плотности локализованных состояний и т.д.), можно рассчитать профиль барьера, и, наоборот, по экспериментально измеренному распределению поля в ОПЗ на контакте Me/a-Si:H можно рассчитать параметры полупроводника [44].
При традиционном способе отсчета координаты от поверхности в глубь полупроводника ход электростатического потенциала и профиль электрического поля рассчитываются по (84) и (85):
;
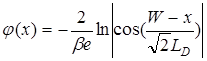(84)
,
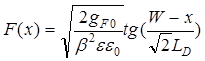(85)
где W рассчитывается по (83) (рис. 26) [45].
Вблизи внутренней границы ОПЗ, так же как и для кристаллов, следует учитывать вклад электронов в формирование объемного заряда. Полагаем, что изгиб зон здесь незначительный, т.е. можно считать ej ~ kT. В этом случае слагаемые в формуле (76), содержащие экспоненциальную функцию, можно разложить в ряд и ограничиться двумя первыми членами [11]:
;
(86)
.
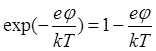(87)
С учетом (86) и (87) формулу (76) переписываем в следующем виде:
.
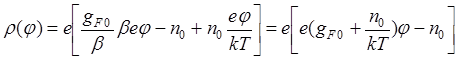(88)
Типовые значения плотности локализованных состояний вблизи уровня Ферми и концентрация свободных носителей заряда для нелегированного a-Si:H следующие: gF0 ~ 1016 эВ-1см-3; n0 ~ 1010 см-3 [6];
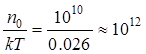эВ-1см-3.
Очевидно, что n0/kT << gF0, поэтому можно пренебречь n0/kT по сравнению с gF0 в формуле (88). С учетом вышесказанного уравнение Пуассона (69) записываем в следующем виде:
.
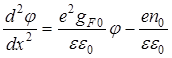(89)
Решение этого дифференциального уравнения с учетом граничных условий (1*, 3*) позволяет получить распределение электростатического потенциала j(x) вблизи внутренней границы ОПЗ:
.
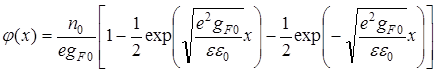(90)
Окончательно выражение (90) можно записать следующим образом:
.
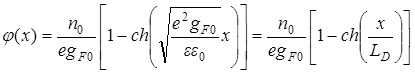(91)
Используя формулу (91), можно рассчитать толщину квазинейтральной области, которая распространяется от точки, где значение электростатического потенциала сравнимо со значением теплового потенциала (φТ = 0.026 В), до внутренней границы ОПЗ:
.
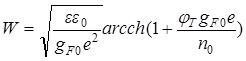(92)
Тогда при традиционном способе отсчета координаты от поверхности полупроводника вглубь формулу (92) можно переписать следующим образом, при условии, что поверхностный потенциал j0 ≈ jT:
,
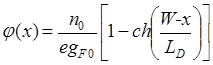где W – толщина квазинейтральной области, которая рассчитывается по (92).
Анализ (93) показывает, что область пространственного заряда в типичных пленках нелегированного a-Si:H распространяется на 2 – 3 мкм (рис. 27) [42]. Обычно в приборостроении используются пленки толщиной порядка 1 мкм [3, 38], поэтому при рассмотрении контактных явлений в тонкопленочных структурах следует говорить не о нейтральной, а о квазинейтральной области. Ход потенциала при незначительном изгибе зон определяется плотностью локализованных состояний вблизи уровня Ферми gF0 и концентрацией электронов проводимости n0 (рис. 5).
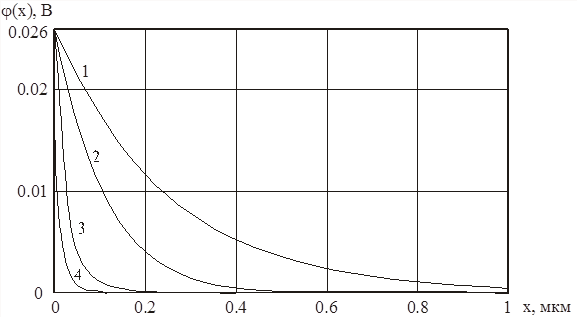
Рис. 27. Ход электростатического потенциала вблизи внутренней границы ОПЗ. Параметры аппроксимации распределения ПС в a-Si:H те же, что и на рис. 26; ширина ОПЗ: 1 - W = 2,70 мкм; 2 - W = 1,04 мкм; 3 - W = 0,38 мкм; 4 - W = 0,14 мкм
2.4. Барьерные эффекты
2.4.1. Фундаментальные ограничения физических размеров барьерных структур
Исходя из соотношений между шириной ОПЗ W, длиной свободного пробега носителей l, длиной волны электрона l и вероятным размером структуры металл-полупроводник d, можно выделить несколько случаев барьера Шоттки:
1) d > W, l, l – для структуры размерные эффекты, связанные с изменением d, не проявляются;
2) W ≥ d > l, l – характеристики структур зависят от их геометрических размеров;
3) l > d, W > l – появляется баллистический эффект, изменяется физика работы структур;
4) W, d ≤ l – проявляются квантовые эффекты, физика работы структур меняется существенно.
По оценкам автора работы [30] для c-Si n-типа необходимо, чтобы ширина ОПЗ превышала длину свободного пробега приблизительно в пять раз (W > 0,043 мкм) для того, чтобы было возможно использование диффузионной теории. При меньших W выполняется диодная теория до значений, при которых станет существенным туннелирование носителей через ОПЗ. Пренебрежение туннелированием приводит к достаточно малым предельным значениям W, при которых структуры остаются выпрямляющими. Но при этом существенно изменяется вид ВАХ. Поэтому высота барьера, найденная из ВАХ и рассчитанная теоретически, в данном случае будут сильно отличаться.
При малых W существенными становятся ограничения, связанные с дискретностью заряда в ОПЗ. Как известно, при решении уравнения Пуассона используется предположение о непрерывном распределении заряде в ОПЗ, но заряд, связанный с ионизированными примесями, является дискретным. Поэтому должно выполняться условие
W >> (Nd)-1/3, (94)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.