Физические процессы в барьерных структурах на основе неупорядоченных полупроводников: Учебное пособие, страница 13

Плотность тока из металла в полупроводник (J_M-S) не зависит от приложенного напряжения и при V = 0 равна:

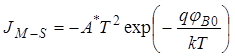.                             (34)

При учете сил зеркального изображения ВАХ диода Шоттки можно записать в следующем виде:

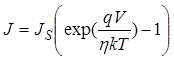,                                      (35)

где ток насыщения J_S определяется по (36), а понижение эффективной высоты барьера Dj по (37):

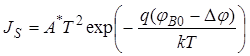,                            (36)

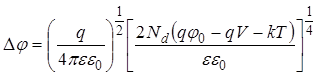.                    (37)

Здесь h – коэффициент неидеальности ВАХ; e – диэлектрическая проницаемость полупроводника; N_d – концентрация ионизированных примесей; j₀ – встроенный диффузионный потенциал.

Коэффициент h может быть определен из экспериментальных ВАХ:

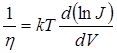,       (при условии V > 3kT/q).                      (38)

Анализ влияния на силы изображения концентрации примеси в полупроводнике показывает, что для N_d < 10²³ м^-3 влиянием сил изображения на прямую ветвь ВАХ можно пренебречь [29]. Однако при обратных смещениях это влияние может оказаться существенным вследствие более сильного электрического поля в обедненной области.

Х. Хениш и Е. Шпенке [29] предложили иной вывод формулы для ВАХ при термоэлектронной эмиссии. Они предполагали, что электроны имеют максвелловское распределение по скоростям на краю обедненной области (х = W). Кроме того, число электронов, преодолевающих барьер, рассчитывалось в предположении, что средняя длина свободного пробега электронов велика по сравнению с шириной ОПЗ (W). Полученное при этом выражение для плотности тока было идентично выражению (35) и имело вид:

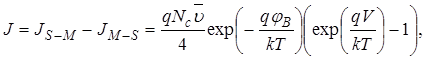              (39)

где  – средняя дрейфовая скорость электронов.

Когда толщина запирающего слоя на контакте металл – полупроводник значительно больше длины свободного пробега электронов, такой слой называют толстым. При расчете плотности тока через толстый барьерный слой необходимо учитывать как дрейфовую, так и диффузионную составляющие. Определять плотность тока из полупроводника в металл как плотность тока термоэлектронной эмиссии через барьер в этом случае нельзя, т.е. диодная теория неприемлема. В литературе теория выпрямления в толстом запирающем слое получила название диффузионной теории выпрямления и обычно связывается с именем Шоттки.

В соответствии с диффузионной теорией концентрация электронов проводимости в полупроводнике в непосредственной близости к границе раздела не меняется при приложении напряжения смещения. Это равносильно предположению, что на границе раздела квазиуровень Ферми в полупроводнике совпадает с уровнем Ферми в металле, т.е. квазиуровень Ферми изгибается вниз в пределах обедненной области полупроводника (рис. 15).

В диффузионной теории используются следующие граничные условия:

- высота барьера много больше кТ;

- рассеяние электронов при их движении в обедненном слое играет существенную роль;

- концентрация носителей при х = 0 и х = W не зависит от протекающего тока;

- концентрация примесей в полупроводнике достаточно мала, и вырождение отсутствует.

ВАХ контакта Шоттки в соответствии с диффузионной теорией выводится из формулы плотности тока в обедненной области:

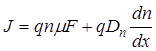,                                      (40)

где первый член суммы – дрейфовая компонента, второй – диффузионная компонента; n – концентрация электронов в полупроводнике n – типа; m – их подвижность; D_n – коэффициент диффузии электронов; F – напряженность электрического поля в ОПЗ; q – заряд электрона.

Необходимо учесть, что формула (40) справедлива в том случае, если подвижность и коэффициент диффузии не зависят от электрического поля. Это предположение не выполняется в эквипотенциальной области, где потенциал (j _b) и напряженность электрического поля достигают своего максимального значения. Кроме того, если функция распределения электронов заметно меняется на длине свободного пробега, что имеет место вблизи (j _b), то нельзя разделять ток на независимые дрейфовую и диффузионную составляющие.

Принимая вышеупомянутые предположения и ограничивая ими точность анализа, можно вывести окончательную формулу для ВАХ барьера Шоттки [30]:

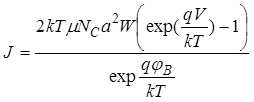,                             (41)

где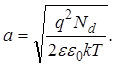

Формулу (41) можно записать в виде:

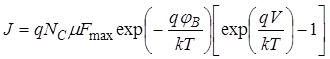,                   (42)

поскольку по теореме Гаусса максимум электрического поля определяется выражением:

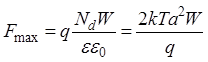.                                (43)

Уравнение (43) является выражением для ВАХ в приближении диффузионной теории. Это уравнение близко по виду, но не полностью совпадает с уравнением для идеального диода.

2.2.4. Теория термоэлектронной эмиссии-диффузии

Группа ученых В. Шульц, Б.Р. Госсик, К.Р. Кроуэлл и С.М. Зи объединили диодную и диффузионную теории, рассмотрев оба механизма последовательно. Наиболее полно эта теория была развита Кроуэллом и Зи [9]. Они учли скорость рекомбинации u_r на границе металл-полупроводник. В этой теории также учитываются рассеяние на оптических фононах, квантово-механическое туннелирование и отражение.

Величина u_r определяется из выражения чистого электронного потока в металл  где n₀ – равновесная концентрация электронов в эквипотенциальной области, в которой потенциал достигает своего максимального значения при нулевом смещении. Члены u_rn и u_rn0 представляют собой потоки электронов из полупроводника в металл и обратно соответственно (рис. 16).

В области между х_м и W величина плотности тока определяется следующим выражением:

                                     (44)

где m_n – подвижность электронов; E_Fn  - энергетическое положение квазиуровня Ферми для электронов, эВ; а N – плотность электронов в точке х, определяемая по формуле 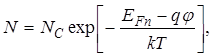(45):

                                  (45)

где N_C – плотность состояний вблизи дна зоны проводимости.

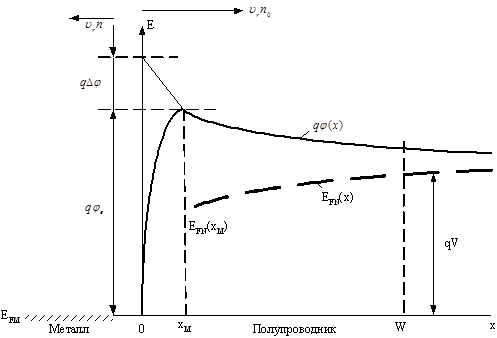
Рис. 16. Энергетическая диаграмма контакта металл-полупроводник при термоэлектронной эмиссии-диффузии: qj(x) – потенциальная энергия электронов; E_Fn – квазиуровень Ферми для электронов

Уравнение (44) не выполняется на участке от 0 до х_м, т.к. потенциальная энергия на этом участке, соизмеримым с длиной свободного пробега, резко возрастает. Эта область работает как сток электронов. Поэтому можно записать следующее выражение:

                                          (46)