Метастабильные дефекты при освещении могут возникать не только в результате превращений "слабые связи Si – Si ® дефект", но и благодаря переходу между дефектами различной природы [1]. При этом исходные дефекты обусловлены технологией получения материала либо возникают в процессе деградации материала под действием света и впоследствии являются источниками для образования более высокоэнергетических метастабильных дефектов.
ГЛАВА 2. ОСОБЕННОСТИ ФОРМИРОВАНИЯ ПОТЕНЦИАЛЬНЫХ БАРЬЕРОВ В НЕУПОРЯДОЧЕННЫХ ПОЛУПРОВОДНИКАХ
2.1. Типы потенциальных барьеров в кристаллических и
неупорядоченных полупроводниках
Микрочастицы в твердых телах обладают потенциальной энергией вследствие их межмолекулярного и кулоновского взаимодействий. Ход потенциальной энергии частицы в зависимости от координаты представляет собой потенциальный рельеф для этой частицы в заданном объеме. В частности, свободные электроны электрически взаимодействуют с узлами кристаллической решетки твердого тела.
В идеальных кристаллах, для которых характерно периодическое расположение атомов или ионов, наблюдается периодический потенциальный рельеф для электронов. В некристаллических материалах эта периодичность нарушается, но основные свойства сохраняются такие же, как у их кристаллических аналогов. Потенциальные барьеры и ямы возникают для электронов при контакте различных материалов, а также на поверхности твердого тела. В частности, тонкий диэлектрический слой, контактирующий с полупроводником, можно представить в виде прямоугольного потенциального барьера, имеющего такую же толщину, как и диэлектрик. Кстати, такой барьер является наиболее простым для математического описания.
В зависимости от вида контактирующих материалов зонные диаграммы и электрофизические характеристики таких барьеров будут отличаться (рис. 10). Наиболее интересными с точки зрения практического использования являются барьеры на контакте металл - полупроводник (рис. 10, а), контакт полупроводников с различным типом проводимости (рис. 10, б), p-i-n структуры (рис. 10, в), а также гетеропереходы (рис. 10 ,г) [11].
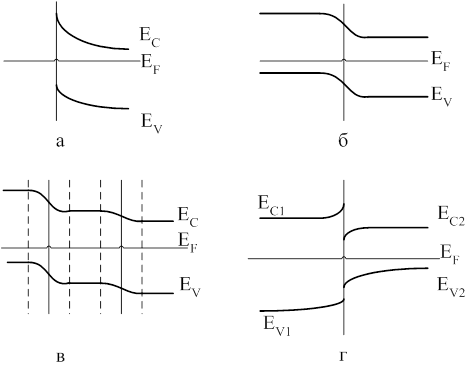
Рис. 10. Энергетические зонные диаграммы контактов твердых тел: а – контакт металл – полупроводник; б – p-n переход; в – p-i-n структура; г – гетеропереход
2.2. Потенциальные барьеры в кристаллических полупроводниках
2.2.1. Модель формирования потенциального барьера на контакте металл - кристаллический полупроводник
Рассмотрим контактные явления для металла и полупроводника, разделенных тонким вакуумным зазором. Предполагается, что эти материалы нейтральны, и поверхностные состояния отсутствуют. На рис. 11, а изображена энергетическая зонная диаграмма для металла и полупроводника n-типа, на рис. 11, б схематически показаны изменение состояния электронов и возникновение контактной разности потенциалов. На рис. 12 схематично изображены системы разрешенных энергетических состояний для металла и полупроводника [24].
Положение энергетических уровней зависит от координаты. Для удобства энергию будем соотносить с энергией свободного электрона (или электрона в вакууме) E0. Разность E0 – EF называется работой выхода, она выражается в единицах энергии и обозначается qj. Напомним, что термодинамическая работа выхода электронов из твердого тела определяется как работа, которую нужно затратить, чтобы перевести электрон с уровня Ферми в вакуум. На рис. 11 уровень энергии в вакууме E0 изображен сплошной линией, а уровни Ферми в металле EFM и в полупроводнике EFS – пунктирными линиями.
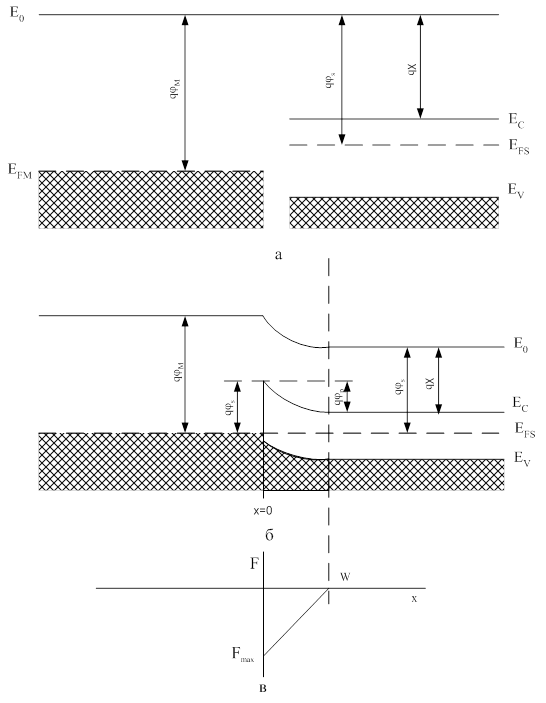
Рис. 11. Образование барьера на границе раздела металл-кристаллический полупроводник (барьера Шоттки): а – зонная диаграмма для изолированных друг от друга металла и полупроводника; б – идеализированная равновесная зонная диаграмма барьера Шоттки; в – распределение поля в идеализированном барьере Шоттки
В полупроводниках работа выхода E0 – EFS зависит от концентрации легирующей примеси, т.к. при изменении степени легирования EFS изменяет свое положение в запрещенной зоне между дном зоны проводимости EC и потолком валентной зоны EV. В то же время разность E0 – EC для данного материала – величина постоянная. Она называется сродством к электрону, выражается в единицах энергии и обозначается qc [28].
В рассматриваемом случае работа выхода электрона из металла qjM больше работы выхода из полупроводника qjS. Это означает, что электроны в полупроводнике обладают более высокой средней суммарной энергией, чем средняя суммарная энергия электронов в металле. Если между двумя материалами установить тесный контакт, то различие в средних энергиях приведет к переходу электронов из полупроводника в металл. Этот переход будет происходить до тех пор, пока не будет достигнуто термодинамическое равновесие в единой системе "металл – полупроводник", т.е. когда уровни Ферми в обоих материалах сравняются.
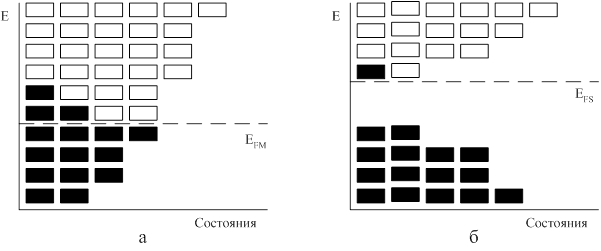
Рис. 12. Системы разрешенных энергетических состояний: а – металл; б – полупроводник (темный цвет – состояния заняты электронами; светлый – свободные состояния)
На рис. 11, б видно, что на границе раздела металл – полупроводник (x = 0) для разрешенных состояний имеется резкий скачок по энергии. Величина этого скачка равна qjВ – высота потенциального барьера со стороны металла:
![]() . (15)
. (15)
В полупроводнике вблизи границы раздела электроны имеют более высокие энергии, чем электроны, находящиеся в объеме материала. Это является следствием переноса отрицательных зарядов из полупроводника в металл. При достижении термодинамического равновесия полупроводник, потерявший электроны, заряжается положительно относительно металла. При этом в приконтактной области полупроводника возникает электрическое поле (рис 11, в), и в результате суммарная потенциальная энергия электронов в полупроводнике увеличивается. Количество свободных электронов вблизи перехода уменьшается, это видно из увеличения расстояния между дном зоны проводимости EC и уровнем Ферми EFS.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.