В этом случае в неупорядоченных полупроводниках возникает совершенно новая ситуация, связанная с появлением конечной и непрерывной плотности локализованных состояний. Как подчеркивал Мотт, в отличие от кристаллов "…новым является представление о том, что может существовать конечная и непрерывная плотность состояний N(E), в которой все состояния локализованы, хотя волновые функции соседних состояний могут перекрываться".
Состояние микрочастицы описывается уравнением Шредингера, которое для одномерного случая имеет следующий вид:
,
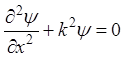(5)
где y - волновая функция, описывающая вероятность нахождения частицы в той или иной области потенциальной ямы, k – волновое число [11].
Необходимо отметить, что в случае одномерной модели непериодической решетки все собственные функции одноэлектронного уравнения Шредингера локализованы, а в случае трехмерной - необязательно. Всякое сколь угодно малое нарушение периодического потенциала в одномерном пространстве вызывает отражение электронной волны, тогда как в трехмерном пространстве возможно огибание волной локального нарушения. Только при достаточной мощности потенциальной ямы, т. е. при достаточном значении произведения ее глубины на квадрат радиуса, локальный уровень может возникнуть даже при отсутствии примесей. Для полупроводников с ковалентной связью нарушение симметрии за счет растяжения валентной связи приводит к возникновению потенциальной ямы для электронов в зоне проводимости и потенциального горба в валентной зоне [12, 13].
Если концентрация локальных возмущений Nt возрастает, то среднее расстояние R между ними уменьшается как N-1/3 [14]. С ростом Nt волновые функции локализованных состояний могут перекрываться, что приводит к обменному взаимодействию между локализованными состояниями. Вследствие этого дискретный уровень энергии Еi расщепляется в зону энергий. В приближении сильной связи [15]
,
(6)
где DЕ – ширина зоны; z – координационное число; I – интеграл перекрытия, зависящий от формы ямы. Согласно работе [16]
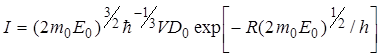, (7)
где Е0 – энергия ионизации уровня; m0 – эффективная масса электрона в изолированной яме; D0 – глубина ямы; V – объем, в котором потенциальная энергия каждой ямы отлична от нуля; R - расстояние между ямой и ближайшим соседом. Определение понятия локализации было дано П. В. Андерсоном в работе [17] следующим образом: состояния локализованы, если электрон с энергией E ± ΔE, помещенный в объем V достаточно большой, чтобы удовлетворить принципу неопределенности, не диффундирует из области локализации. Таким образом, состояния являются локализованными в том смысле, что электрон, введенный в некоторую область пространства при нулевой температуре, не может продиффундировать в другие области с такими же флуктуациами потенциала.
Флуктуационные уровни в аморфных полупроводниках играют роль ловушек для электронов и дырок. Они аналогичны по происхождению уровням дефектов кристаллической решетки типа пустого узла или атома в междоузлии, но существенно отличаются от последних. В случае бесконечной системы атомной решетки возникают хаотические флуктуации амплитуды и фазы волновой функции при переходе от ямы к яме, и соответственные значения энергии в запрещенной зоне образуют квазинепрерывный спектр.
Помимо дефектов, связанных с нарушением периодичности за счет флуктуационных искажений потенциала, к появлению локализованных состояний могут привести примеси внедрения и замещения, атом основного вещества в междоузлии решетки, дислокации, поверхностные состояния и другие, характерные и для кристаллических полупроводников нарушения структуры [15]. Степень локализации их в принципе ничем не отличается от рассмотренной выше. Отметим, что поверхностные состояния для аморфных полупроводников следует понимать не только как состояние наружной поверхности; необходимо учитывать и внутреннюю поверхность пор. Особенно это относится к аморфным пленкам, плотность которых, как правило, ниже, чем у кристаллов. Надо полагать, что при отжиге, увеличивающем плотность вещества, количество локализованных состояний уменьшается [16].
Образование дополнительных локализованных состояний возможно за счет взаимодействия электрона с индуцированным им положительным зарядом, что приводит к возникновению дополнительной потенциальной ямы, локализующей электрон. Система, состоящая из электрона и поляризованной им области, носит название полярона. Появление полярона более вероятно в веществах с преобладающей ионной связью. Энергия полярона задается выражением [1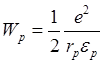8]:
, (8)
где 
– эффективный радиус полярона:
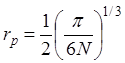, (9)
где N – число потенциальных ям в единице объема; 
– приведенное абсолютное
значение диэлектрической проницаемости:
,
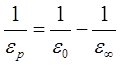(10)
здесь
и 
– статическое и высокочастотное значения
диэлектрической проницаемости. Значение Wp получается
отрицательным по знаку. Степень взаимодействия электронов с решеткой и
возможность образования поляронов характеризуются постоянной связи:
,
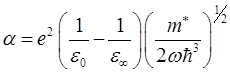(11)
где w - угловая частота оптических фононов; m* - эффективная масса в невозмущенной решетке.
Различают два вида поляронов: малого радиуса – с линейным размером порядка постоянной решетки и большого радиуса – у которых a » 7 ¸ 8 в случае сильной связи [16, 19]. Однако четкого различия между поляронами малого и большого радиуса нет.
В качестве еще одной интересной особенности аморфных полупроводников отметим, что такие понятия, как "потолок валентной зоны", "дно зоны проводимости", "запрещенная зона" для неупорядоченных материалов имеют несколько иной смысл, чем для кристаллических. Н. Мотт [15] впервые ввел понятие критических энергий ЕС и ЕV, отделяющих локализованные состояния от нелокализованных. При этом, по аналогии с принятой терминологией для кристаллов, EC считается граничным уровнем для зоны проводимости, ниже которого расположены локализованные состояния, а выше – нелокализованные, т. е. ЕC – "дно" зоны проводимости; EV – граничный уровень для валентной зоны, выше которого состояния локализованы, а ниже – не локализованы, т. е. EV – "потолок" валентной зоны. Интервал энергетического спектра ΔE = ЕC – EV применительно к аморфным полупроводникам называют запрещенной зоной по подвижности, или щелью подвижности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.