На рис. 21, а приведена зонная диаграмма для равновесного состояния p-n перехода. Уровень Ферми является общим для всех областей полупроводника. При переходе из n- в p-область потенциал уменьшается на величину контактной разности потенциалов. Значение Vконт можно определить из следующей формулы:
,
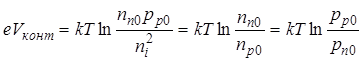(63)
где ni – собственная концентрация, nn0 и pp0 – концентрации основных носителей заряда в n- и p-областях соответственно, np0 и pn0 – концентрации неосновных носителей соответственно.
Чем сильнее легированы обе области полупроводника, тем больше контактная разность потенциалов. Теоретически максимальное значение eVконт в невырожденных полупроводниках равно ширине запрещенной зоны.
При наложении внешнего поля равновесие нарушается, и уровни Ферми заменяются на квазиуровни. Полем в толще полупроводника обычно пренебрегают, т.е. считают, что практически все внешнее напряжение падает на p-n переходе.
При наложении внешнего поля в прямом направлении изгиб зон на p-n переходе уменьшается и равен e(Vконт –V), квазиуровни Ферми для основных носителей заряда двигаются относительно друг друга на eV (рис. 21, б). При наложении внешнего поля в обратном направлении изгиб зон на p-n переходе увеличивается и равен e(Vконт +V) (рис. 21, в).
Общая ширина p-n перехода определяется как сумма толщин ОПЗ, приходящихся на n- и p-области. Толщина p-n перехода пропорциональна напряжению и обратно пропорциональна концентрации легирующей примеси. Для резкого перехода толщина будет определяться следующей формулой:
.
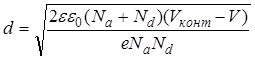(64)
В случае плавного симметричного перехода толщина определяется следующим образом:
,
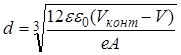(65)
где An = Ap = A – градиент концентрации легирующих примесей.
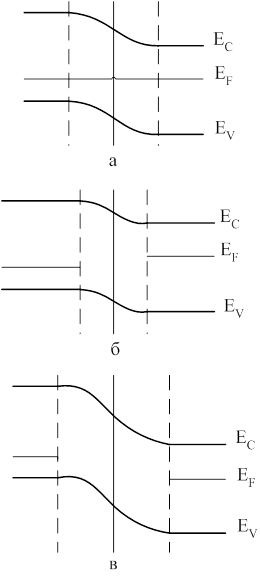
Рис. 21. Зонная диаграмма p-n-перехода при различных смещениях: а – равновесное состояние; б – прямое смещение; в – обратное смещение
Электронно-дырочный переход представляет собой высокоомную область, т.е. аналог диэлектрика. Таким образом, p-n переход эквивалентен конденсатору, обкладками которого являются границы p-n перехода, а в качестве диэлектрика выступает сам запирающий слой.
Барьерная емкость p-n перехода определяется аналогично емкости плоского конденсатора, т.е.
,
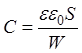(66)
где S – площадь перехода. Для резкого p-n перехода:
,
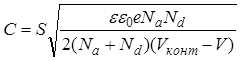(67)
для плавного симметричного p-n перехода:
.
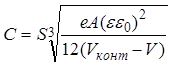(68)
Кроме барьерной емкости, p-n переход при прямом включении имеет еще диффузионную емкость, связанную с переносом носителей заряда через барьер.
2.3. Потенциальные барьеры в неупорядоченных полупроводниках
2.3.1. Модель формирования потенциального барьера на контакте металл - неупорядоченный полупроводник
Как отмечалось ранее, неупорядоченные полупроводники и, в частности, аморфный гидрогенизированный кремний характеризуются высокой плотностью состояний, локализованных в щели подвижности, которая может превосходить плотность поверхностных состояний [34]. Это обусловливает отличия электрофизических свойств неупорядоченных материалов от кристаллических, в том числе оказывает определяющее влияние на процесс формирования барьера металл - неупорядоченный полупроводник.
Барьеры на аморфных полупроводниках отличаются от кристаллических прежде всего тем, что плотность заряда r(x) и ход потенциала j(х) в ОПЗ определяются не только ионизированными примесями, как у кристаллических полупроводников, но и распределением плотности локализованных состояний в щели подвижности.
Свойства барьера металл - некристаллический полупроводник значительно отличаются от свойств классического барьера Шоттки. Это очевидно, т.к. физическая природа полупроводников различается. Поэтому ведутся активные поиски физико-математической интерпретации свойств барьера металл - некристаллический полупроводник.
В настоящее время существует несколько моделей, описывающих формирование этого барьера.
Модель
активационного барьера.
Была впервые предложена авторами [35] для контакта металл - ХСП. Суть этой
модели заключается в следующем. После приложения электрического поля носители
(в данном случае дырки), освобождающиеся с ловушек вследствие термической активации,
дрейфуют к катоду, и при отсутствии инжекции с контакта вблизи анода возникает
область объемного заряда электронов (рис. 22). В условиях термического
равновесия энергетическая плотность захваченных носителей заметно отличается от
нуля только вблизи уровня Ферми. Поэтому носитель, активизированный в зону
проводящих состояний, прежде чем будет снова захвачен на глубокую ловушку и
вернется в термическое равновесие, несколько раз испытает акты захвата и
освобождения на более мелких ловушках и пройдет значительное расстояние по зоне
проводящих состояний. Это расстояние на начальном интервале времени 0 ≤ t ≤ t1 определяет толщину слоя объемного заряда х*(t) (рис. 22, а). Плотность
объемного заряда электронов n(t) и профиль поля F определяются положением демаркационного
уровня 
выше которого ловушки уже пусты, а
ниже – их заселенность остается еще равновесной. Увеличение толщины заряженного
слоя продолжается до тех пор, пока либо слой занимает весь образец, либо
объемный заряд слоя полностью экранирует приложенное электрическое поле. Во
втором случае поле переносит освобождающиеся носители к границе слоя, и внутри
него плотность заряда продолжает возрастать. На границе слоя поле обращается в
нуль, дрейф носителей прекращается, и опустошенные ранее ловушки заполняются
носителями, прибывающими из области объемного заряда (рис. 22, б).
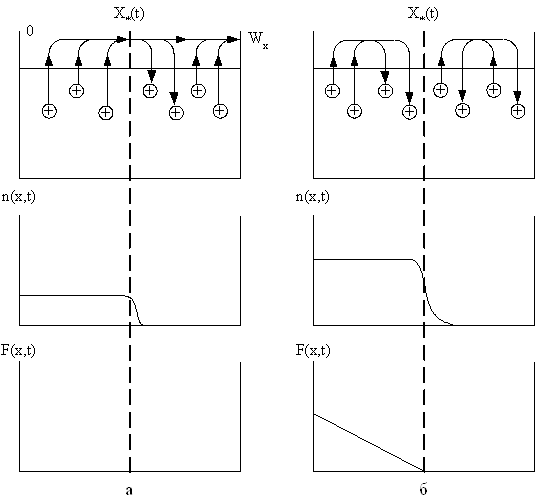
Рис. 22. Кинетика формирования активационного барьера: а – начальная стадия формирования; б – конечная стадия формирования барьера
В результате при t > t1 толщина заряженного слоя убывает. Если же область объемного заряда успевает занять весь образец раньше, чем приложенное поле будет экранировано полем ОПЗ, образец остается почти однородно заряженным до момента, пока поле не обратится в нуль на катоде. В описанном механизме процессы диффузии приводят к небольшому размытию границы слоя ОПЗ вблизи х = х*(t). При уменьшении толщины слоя возрастает градиент плотности, и диффузия начинает играть более заметную роль в распределении пространственного заряда. Через время t >> t1 конкуренция дрейфа и диффузииприводит к установлению стационарного распределения плотности заряда. Из описания этой модели вытекают следующие выводы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.