Величина fq для Si и GaAs больше 1 для F > 4×106 В/м вследствие эффекта туннелирования. Для меньших полей fq < 1 вследствие отражения и приближается к 0,6 для GaAs и 0,5 для Si. Величина А** не является строго постоянной, т.к. зависит от приложенного поля. Однако этот эффект маскируется в эксперименте эффектом Шоттки и другими эффектами.
При 300К А** = 112×104 А×м-2×К-2 (Si <111>, n-тип);
А** = 32×104 А×м-2×К-2 (Si, p-тип);
А** = 4.4×104 А×м-2×К-2 (GaAs).
2.2.7. Влияние глубоких центров на параметры ОПЗ
Глубокие центры (ГЦ), т.е. центры, образующие в запрещенной зоне полупроводника глубокие энергетические уровни, существуют в полупроводнике из-за наличия примесей, радиационных и механических дефектов, дефектов термообработки и т.д.
Рассмотрим влияние ГЦ на параметры ОПЗ. Пусть в полупроводнике существуют, кроме основной примеси с концентрацией Nd, два однозарядных ГЦ с соответствующими концентрациями N1 и N2. Этим центрам соответствуют энергетические уровни Е1 и Е2 соответственно (рис. 18, а). При отсутствии внешнего напряжения заполнение электронами обоих уровней определяется их положением относительно уровня Ферми. Каждый из уровней заполнен электронами там, где он расположен ниже уровня Ферми, т.е. уровень Е1 заполнен электронами при х > w1, а Е2 – при х > w2 (рис. 18, а). Уход электронов с уровня Е1 приводит к возрастанию концентрации ионизированных центров в ОПЗ независимо от того, является ли ГЦ донором или акцептором. Поэтому распределение концентрации в начальный момент времени будет выглядеть, как показано на рис. 18, б. Если концентрация ионизированных центров (мелких и глубоких) не зависит от координаты по всей ширине ОПЗ, то значения j и N можно вычислить из (20) и (31) соответственно. Можно заметить также, что для большой концентрации ГЦ, сравнимой с концентрацией основной примеси, ширина ОПЗ несколько уменьшается, т.к. в знаменателе в выражении (31) вместо Nd входит сумма (Nd + N1 + N2) при условии, что Е1 и Е2 являются донорными.
Влияние ГЦ на переходные процессы в барьерах Шоттки и емкость барьеров детально рассматривается в работах [29, 30, 32, 33].
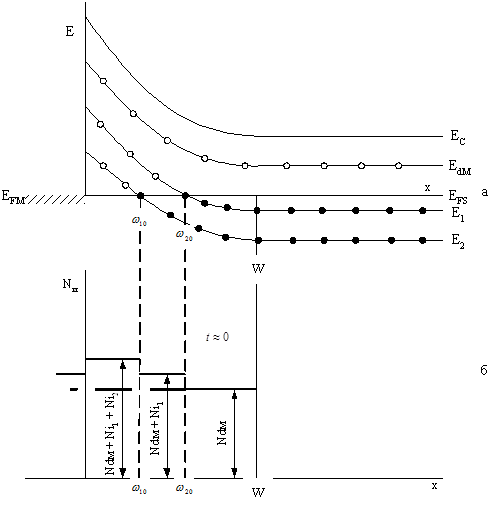
Рис. 18. Энергетическая модель структуры металл-полупроводник n-типа в отсутствии смещения и в приближении полного обеднения (а); изменение концентрации ионизированных примесей (Nи) от координаты х (б)
2.2.8. Барьер Мотта
Кроме физического запирающего слоя, каким является барьер Шоттки, существуют также химические и технологические слои, связанные с наличием на поверхности полупроводника слаболегированного тонкого слоя. Этот тип контакта был исследован Н. Моттом, рассмотревшим его в связи с изучением диодов на основе оксидных соединений.
В случае барьера Мотта полупроводник характеризуется резким изменением уровня легирования от низкого значения вблизи границы раздела с металлом до высокого значения на очень близком расстоянии от поверхности, которое много меньше длины Дебая LD. Так как длина слаболегированной области очень мала, то электрическое поле в ней может рассматриваться как постоянное. Предполагается, что силовые линии не проникают в сильнолегированную область, т.к. концентрация доноров в ней очень велика. Таким образом, зонная диаграмма будет выглядеть, как показано на рис. 19.
ВАХ барьера Мотта имеет вид:
,
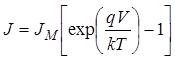(59)
где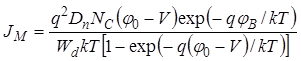 
. (60)
Ток насыщения барьера Мотта JM сильнее зависит от прикладываемого напряжения, чем JS – ток насыщения барьера Шоттки. Оба выражения, полученные для токов насыщения JS (36) и JM (60), теряют физический смысл при приближении прямого напряжения к j0 – встроенному потенциалу. На практике, если бы прямое напряжение, приложенное к диоду, было равно j0, то вблизи перехода барьер бы отсутствовал, и через контакт могли протекать очень большие токи, ограниченные только последовательным сопротивлением полупроводника. Реальное напряжение, приложенное к барьеру Шоттки в прямом направлении, на практике никогда не достигает величины встроенного потенциала.
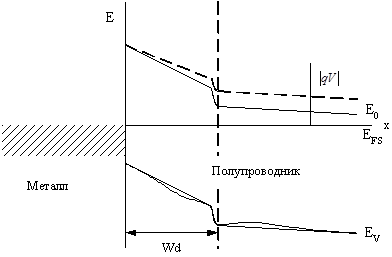
Рис. 19. Энергетическая диаграмма барьера Мотта: Wd – толщина слаболегированной области; V – прямое напряжение
2.2.9. Классическая модель формирования ОПЗ в p-n- переходах
на кристаллических полупроводниках
Электронно-дырочным переходом (p-n переходом) называют слой полупроводника, располагающийся по обе стороны от границы раздела p- и n-областей, обедненных основными носителями заряда и представляющих собой запирающий слой.
В зависимости от характера распределения примесей различают два крайних случая – резкий (ступенчатый) и плавный p-n переходы. В резком p-n переходе концентрация доноров и акцепторов изменяется скачкообразно на границе раздела p- и n-областей, а в плавном переходе их концентрация является линейной функцией от расстояния (рис. 20). Относительно резкий p-n переход можно создать в кристалле эпитаксиальным наращиванием и ионным легированием, плавный – при диффузии.
В зависимости от степени легирования p- и n-областей различают симметричный и несимметричный p-n переходы. В симметричном переходе концентрации доноров и акцепторов приблизительно одинаковые, в резких – концентрации значительно отличаются.
В теории p-n перехода обычно считают, что концентрация равновесных носителей заряда в полупроводнике вне p-n перехода равна концентрации примесей, т.е. последние полностью ионизированы. В областях, обедненных основными носителями заряда, объемный заряд определяется ионизированными примесями. Для резкого p-n перехода объемный заряд в n-области определяется как постоянная величина (рис. 20, а):
;
(61)
для плавного – соответственно в виде линейной функции (рис. 20, б):
,
(62)
где An – градиент концентрации ионизированных примесей (доноров).
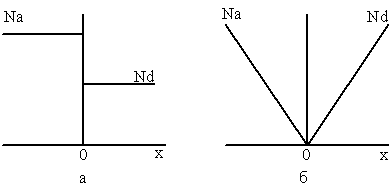
Рис. 20. Распределение примесей на контакте p- и n-областей в резком (а) и плавном (б) переходах
При отсутствии внешнего напряжения p-n переход находится в равновесии. Диффузионные токи основных носителей заряда скомпенсированы дрейфовыми токами неосновных носителей заряда, так что полный ток через p-n переход равен нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.