Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 9

30

8. Определите амплитуды колебаний, при которой их еще можно считать малыми, то есть найдите область амплитуд колебаний, где в рамках точности эксперимента период оборотного маятника не зависит от амплитуды. После этого установите маятник на одну из опор и (аналогично случаю математического маятника) проведите измерение периодов при двух амплитудах колебаний около одной призмы и затем, перевернув маятник, – при двух амплитудах колебаний около другой призмы. Результаты измерений запишите в таблицу 2. Измерьте линейкой расстояние bмежду остриями опор маятника dи также впишите его в таблицу 28. Положите маятник горизонтально на какой-либо острый предмет (например, ребро линейки) и найдите приблизительно положение центра масс - точку, опираясь на которую маятник будет в равновесии. Проверьте, выполняется ли условие d₁¹ d₂ применимости формулы (8).

9. На основе данных, полученных для матема­тического и физического маятников, вычислите значения ускорения свободного падения. Результаты запишите в таблицу 3.

Таблица 3

Математический маятник		Физический маятник
Амплитуда 1	Амплитуда 2	Призма 1			Призма 2
		Амплитуда 1	Амплитуда 2		Амплитуда 1	Амплитуда 2
gм1, м/с2	gм2, м/с2	gф1, м/с2		gф2, м/с2	gф3, м/с2	gф4, м/с2
Округлённые значения ускорения свободного падения
gм1*, м/с2	gм2*, м/с2	gф1*, м/с2		gф2*, м/с2	gф3*, м/с2	gф4*, м/с2

9. Рассчитайте ошибки измерения ускорения свободного падения в обеих сериях экспериментов. Поскольку измерения ускорения свободного падения – косвенные, и преобладающей является ошибка измерения времени, фиксируемого оптодатчиками, соответствующие ошибки рассчитываются как среднеквадратичные.

Среднеквадратичная ошибка s_fизмерения какого-либо параметра f =f(x, y, z…) в общем виде рассчитывается по формуле

s_f=.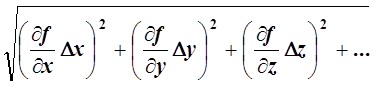

	31

 

Для математического маятника g = 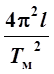 , где Т_м – средние значения периода (T_СР из таблицы 1), следовательно,

s_gм  =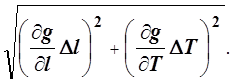

Продифференцировав это выражение по lиT, а также использовав, что Т_м = T_СР, после стандартных преобразований получаем необходимые формулы для расчёта s_gм1 и s_gм2:

s_gм1=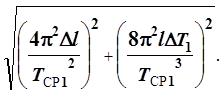                               (9)

В этой формуле Dl – приборная ошибка линейки для измеренияl; DT₁ =0,0005 с – приборная ошибка измерения периода колебаний математического маятника при первом значении амплитуды колебаний (случайная ошибка определения периода мала).

Аналогично рассчитывается ошибка s_gм2 для второго значения амплитуды колебаний математического маятника.

Для оборотного маятника g = 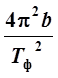, где Т_ф – средние значения периода (T_СР из таблицы 2), следовательно,

s_gф1=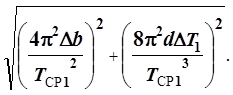                               (10)

В этой формуле Db – приборная ошибка линейки для измеренияb; DT₁ =0,0005 с – приборная ошибка измерения периода колебаний оборотного маятника при первом значении амплитуды колебаний.

32

Таким же образом рассчитывается ошибка s_gф2 измерения ускорения свободного падения при втором значении амплитуды колебаний оборотного маятника на той же призме, после чего вычисляются ошибки s_gф3 и  s_gф4измерения g для двух амплитуд оборотного маятника, колеблющегося на другой призме.

10. Округлите полученные ошибки до первой значащей цифры; до этого же разряда округлите полученные ранее значения ускорения свободного падения и внесите эти значения в таблицу 3.

Итоговые результаты измерений представьте в виде:

	gм1= gм1* ±s gм1 gм2= gм2*  ±sgм2 gф1= gф1* ±sgф1 gф2= gф2*  ±sgф2 gф3= gф3* ±sgф3 gф4= gф4* ±sgф4

 

                                                                                     .

Приступая к работе, помните:

-  включать в сеть измерительный блок L-микро можно только после его подключения к разъему последовательного порта компьютера;

-  с оборотным маятником следует обращаться осторожно: не допускайте падений и ударов ма­ятника, это может нарушить его юстировку.

Контрольные вопросы

1. Какой маятник называется математическим? В каком случае этот маятник совершает колебания с периодом, рассчитываемым по формуле (1)?

2. Какой маятник называется физическим? В каком случае этот маятник совершает колебания с периодом, рассчитываемым по формуле (2)?

33

3. Сформулируйте теорему Штейнера. Как эта теорема используется в настоящей работе?

4. Можно ли определить ускорение свободного падения, если у оборотного маятника расстояния от центра масс до обеих призм одинаковы? Ответ обоснуйте.

5. Выведите формулу для расчёта ускорения свободного падения с помощью оборотного маятника.

РЕКОМЕНДУЕМАЯ  ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

	34		35

 

РАБОТА  № 5-П

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Цель работы: изучение динамики вращательного движения и закона сохранения момента импульса на примере системы с изменяющимся моментом инерции.