Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 7

2. Объясните, из каких соображений в данной работе выбирается число значащих цифр после запятой при округлении результатов вычислений.

3. Выведите формулу (9); укажите возможные причины неко­торого несовпадения величин моментов инерции, определен­ных по этим формулам.

4. Сформулируйте основной закон динамики вращательного движения.

5. При каком положении грузов маховик Обербека раскручивается с наибольшим угловым ускорением? Ответ обоснуйте.

РЕКОМЕНДУЕМАЯ  ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

	23

 

РАБОТА  № A4-П

ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МАЯТНИКОВ

Цель работы: измерение ускорения свободного падения в поле сил тяжести.

Приборы и принадлежности: штатив универсальный, кронштейн, скоба, математический маятник (шарик диаметром 13 мм на нити), оборотный маятник, оптодатчик, линейка, измерительный блок L-микро.

Введение

Математическим маятникомназывается твёрдое тело, подвешенное на нити; массой нити можно пренебречь по сравнению с массой тела; размерами тела можно пренебречь по сравнению с размерами нити; по сравнению с размерами нити можно пренебречь и её возможным удлинением под действием внешних сил.В идеальном случае математическим маятником является материальная точка, подвешенная на невесомой и  нерастяжимой нити. Можно показать, что если углы отклонения j такого маятника от вертикали малы (так, что j»tgj»sinj), то период T_мколебаний (время, за которое совершается одно полное колебание) описывается формулой

Т_м=2p.                                            (1)

Здесь l – длина нити,g – ускорение свободного падения. (При выводе данной формулы предполагается, что на маятник не действует никаких других сил, кроме силы тяжести).

24

Физическим маятником называется абсолютно твёрдое тело, совершающее колебания относительно оси, проходящей через точку, не являющуюся центром тяжести тела. В механике под абсолютно твёрдым понимают тело, которое невозможно деформировать (реально – возможные деформации которого много меньше размеров тела). Если углы отклонения j такого маятника от вертикали малы (то есть j»tgj»sinj), то период T_фего колебаний рассчитывается следующим образом:

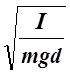Т_ф=2p.                                         (2)

В этой формуле I – момент инерции маятника относительно оси, относительно которой происходят колебания, m – масса маятника, d– расстояние от центра его тяжести до этой оси.

Напомним, что момент инерции тела Iотносительно некоторой оси является мерой инертности тела при вращении его вокруг этой оси. Для материальной точки момент инерции равен произведению ее массы на квадрат расстояния до оси вращения:

I = mr²,

а для тела, которое можно представить в виде системы боль­шого количества материальных точек, момент инерции отно­сительно некоторой оси равен сумме произведений масс всех материальных точек на квадраты их расстояний до этой оси:

I=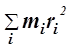  или    I = .

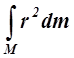Момент инерции зависит как от общей массы тела, так и от его формы, от характера распределения массы по объёму.

Как следует из формул (1) и (2), периоды колебаний математического и физического маятника зависят от ускорения свободного падения: измерив Т_м или Т_ф в эксперименте, с учётом известных значений параметров маятника, можно вычислить, чему равно g.

Если измерение ускорения свободного падения с помощью математического маятника достаточно просто осуществить (и период колебаний и длина маятника легко измеряются):

g= 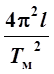  ,                                           (3)

25

то проводить измерения g с помощью произвольного физического маятника уже не так просто. Дело в том, что для этого необходимо знать точное значение момента инерции маятника относительно выбранной оси и положение его центра масс (для измерения расстояния d). Поэтому для определения g используется прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции такого маятника.

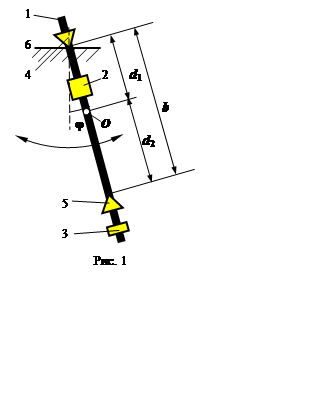Оборотный маятник рис. 1 является физическим маятником, кото­рый устроен следующим образом. На стержне (1) закрепляются два груза (2), (3). Стержень имеет две оси вращения, расположенные, по разные стороны от центра масс (точка О)системы. Осями вращения служат рёбра вершин треугольных призм (4), (5), изготовленных из твердого материала; призмы установлены на специальную опору (6) закрепленную на подставке.

Оборотный маятник регулируется таким образом, чтобы период его колебаний при установке на одной призме равнялся периоду колебаний его на другой призме. Регулировка произ­водится путем изменения взаимного расположения грузов и призм на стержне.

Выведем формулу периода колебаний оборотного маятника. Согласно теореме Штейнера  момент инерции I тела относительно произвольной оси равен сумме момента инерции I₀ этого тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения его массы т на квадрат расстояния d  между осями:

I = I₀ + md².                                         (4)

После подстановки в формулу (2) получим:

Т_ф=2p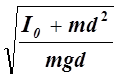.                                   (5)

Поскольку оборотной маятника имеет равные периоды колебаний на обоих призмах (осях), на основании (5) можно записать:

26

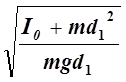
Т_ф =2p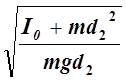

Т_ф=2p.                                        (6)