Физика \ Физика

Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 18

j0, град

j1, град

j2, град

a1, град

a2, град

1

2

…

5

l, м =

M, кг = 0,035

m, кг = 0,016

6. После прекращения записи данных на экране компьютера возникает график зависимости угла отклонения от времени. Вам необходимо определить угол максимального отклонения. Для этого, используя клавиши, следует подвести курсор (вертикальную черту на экране) к интересующей Вас точке графика и записать в таблицу 1 численное значение угла, которое высвечивается на экране.

Линейкой измерьте длину маятника l и запишите результат в таблицу 1. Значения масс маятника M и пульки m в таблицу уже внесены.

67
 
Нулевой угол отклонения маятника (положение равновесия) соответствует произвольному значению угла в диапазоне 90¸ 270°. Поэтому при обработке данных для определения максимального угла отклонения необходимо из значения угла, полученного для первого максимума или минимума кривой на экране, вычесть значение угла, соответствующего положению равновесия (прямая линия на экране, предшествующая движению маятника). Знак угла отклонения при этом, естественно, не имеет физического смысла и может быть опущен.

При выполнении измерений следите за тем, чтобы углы отклонения маятника не выходили за рамки рабочего диапазона датчика угла поворота.

Чтобы убедиться в том, что потери на трение малы, следует также выписать в таблицу амплитуду второго колебания маятника и вычислить величину отклонения в противоположную сторону.

7. Эксперимент и предварительную обработку данных следует повторить 5 раз, а результаты измерений – записать в таблицу 1:

Обозначения, принятые в таблице 1:

j0– угол, измеряемый датчиком и соответствующий положению равновесия;

j1– угол, измеряемый датчиком и соответствующий амплитуде первого отклонения маятника;

 j2– угол, измеряемый датчиком и соответствующий амплитуде второго отклонения маятника;

a1=j1-j0иa2 =j2-j0– истинные значения амплитуд углов первого и второго отклонения соответственно.

8. Рассчитайте среднеарифметические значения углов отклонения a1СР и a2СР, а также Вычислите aСР = (a1СР+ a2СР )/2.; результаты запишите в таблицу 2.

9. Рассчитайте Da1и Da2  – ошибки измерений углов a1и a2:

Da1  =a 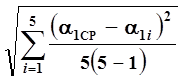,                                      (9)

Da2  =a 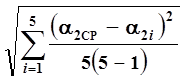,                                   (10)

Здесь a-коэффициент Стьюдента, значения которого можно найти в таблице, приведённой в Приложении к настоящему сборнику (см. также методические указания [3]). Величину доверительной вероятности при выборе коэффициента Стьюдента по этой таблице примите равной 0,95.

68
 
Вычислите DaСР = (Da1+ Da2  )/2.

Результаты вычислений запишите в таблицу 2.

10. Используя средние значения углов a1и a2, а также данные таблицы 1 (о величине l, M и m), по формуле (8) рассчитайте средние значения скорости пульки u1СР и u2СР. В расчётах примите g= 9,81 м/с2.

Результаты вычислений занесите в таблицу 2.

11. Пользуясь полученными значениями u1СР и u2СР, вычислите итоговое значение скорости пульки: uСР = (u1СР + u2СР)/2. Полученное значение средней скорости uСР  также запишите в таблицу 2.

Таблица 2

Da1, град

Da2 , град

aСР ,

град

DaСР ,

град

u1СР,

м/с

u2СР,

м/с

uСР,

м/с

Контрольные вопросы

1. Сформулируйте закон сохранения механической энергии. Можно ли применять этот закон для описания движения маятника в данной работе? Ответ поясните.

2. Сформулируйте закон сохранения импульса. Можно ли применять этот закон для описания движения маятника в данной работе? Ответ поясните.

3. Объясните, из каких соображений в данной работе выбирается число значащих цифр после запятой при округлении результатов вычислений.

4. Выведите формулу (8) для скорости пульки

5. Выведите формулу для расчёта среднеквадратичной ошибки измерения скорости пульки.

РЕКОМЕНДУЕМАЯ  ЛИТЕРАТУРА

69
 
1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высшая школа, 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме / Н.А.Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

70
 
 


РАБОТА  № 11-П

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА

МЕТОДОМ КЛЕМАНА - ДЕЗОРМА

Цель работы: определение величины отношения теплоемкости  воздуха при  постоянном давлении к теплоемкости при постоянном объеме.

Приборы и принадлежности: Клапан, сосуд с герметической пробкой, насос ручной,  соединительные трубки, датчик давления, измерительный блок L-микро

Введение

1. Идеальным называется газ

-  Молекулы которого  можно считать материальными точками (другими словами, размеры молекул много меньше расстояния между ними);

-  Молекулы газа не взаимодействуют на расстоянии, а испытывают лишь упругие столкновения друг с другом (и со стенками сосуда, в котором находятся).

Скачать файл