Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 19

Идеальный газ описывается уравнением Менделеева – Клапейрона:

pV=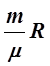T,                                          (1)

где p – давление газа (измеряется в паскалях); V – объём газа (измеряется в кубических метрах); m– его масса (в килограммах); m - масса одного моля газа (в килограммах на моль); T – термодинамическая температура (в кельвинах), R =8,31 кг×моль^-1×К^-1 – универсальная газовая постоянная.

     2. Первое начало (закон) термодинамики утверждает, что количество теплоты dQ, сообщенное системе, расходуется на изменение её внутренней энергии dU и на работу dА, совершаемую системой против внешних сил:

                                               dQ=dU+dA .                                      (2)

Для идеального газа

71

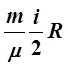dU=dT,                                     (3)

Здесь i – число степеней свободы – число независимых параметров, определяющих положение и ориентацию молекулы в пространстве.

Работа газа связана с изменением dV его объёма:

dA = p dV .                                              (4)

В частности, если давление газа не меняется (такой процесс называется изобарным), то, с учётом уравнения (1), можно получить:

                                               dA=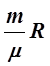dT.                                   (5)

Очевидно также, что при V=constdV= 0   и  dA= 0.

3. Запишем формулы первого начала термодинамики для основных изопроцессов, которые можно осуществить с идеальным газом.

–   Изобарный ( р =const ):

                                   dQ=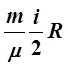dT+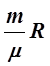dT,  или

                                   dQ=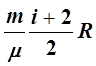dT.                                         (6)

–   Изохорный ( V=const ):

                                           dQ=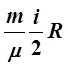dT.                                          (7)

–   Изотермический ( Т =const ):

                                                dQ=pdV.                                               (8)

–  Адиабатный (происходящий без теплообмена с окружающей средой, dQ= 0):

0 =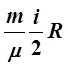dT  + p dV.                                    (9)

4.  Теплоемкостью газаназывается величина равная количеству теплоты, необходимой для нагревания данной массы газа на один кельвин.

с= lim DQ / DT = dQ / dT .                              (10)

DT®0

72

Теплоемкость единицы массы газа называется удельной теплоемкостью с_уд. Теплоемкость С одного моля называется молярной теплоемкостью:

С = с × .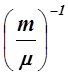

Получим выражения для теплоёмкости газа в изохорном (при постоянном объёме) C_v  и изобарном (при постоянном давлении) C_p процессах.

– При V =const

C_v=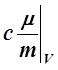==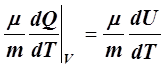.                   (11)

– При р =const

C_p=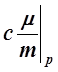==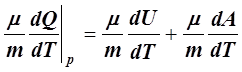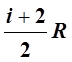.          (12)

Из (11) и (12) следует, что

C_p= C_v  + R.                                          (13)

Соотношение (13) носит название уравнения Майера.

5. Пользуясь уравнением Менделеева – Клапейрона (1), формулами (11) и (12) для C_v и C_p и соотношением (9) – первым началом термодинамики в случае адиабатного процесса, можно получить формулу, связывающую параметры идеального газа при адиабатном процессе. Для этого достаточно продифференцировать обе части уравнения (1) по Т :

p+V=,

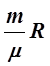откуда

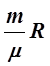dT = pdV + Vdp,

и подставить последнее соотношение в формулу (10). Тогда получится:

0 =( pdV + Vdp)+ p dV,

или

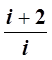pdV+Vdp= 0.

73

Последнее уравнение можно представить в виде

d 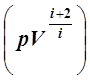 = 0,     или

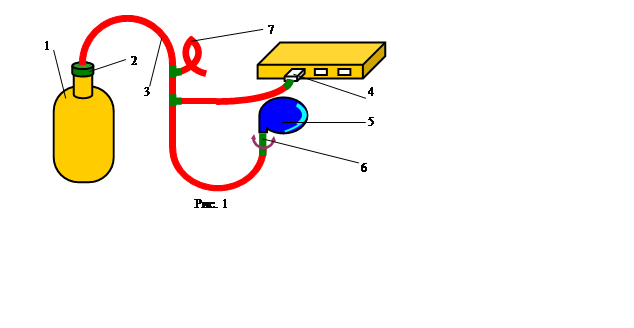
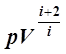 =const.                                       (14)

С учётом того, что

 =,

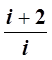формулу (14) можно записать в виде

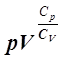 =const.                                        (15)

Данная формула носит название уравнения Пуассона для адиабатного процесса.

Обозначив отношение C_p/ C_v  символом g, уравнение (15) можно переписать:

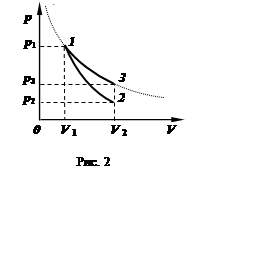pV^g =const.                                          (16)

В настоящей работе предлагается найти показатель степени в уравнении Пуассона для сухого воздуха, который при комнатных условиях с хорошей точностью можно считать идеальным газом.

Методика измерений и описание установки

Для определения отношения С_p/ C_v воздуха в данной лабораторной работе применен метод, предложенный Клеманом и Дезормом, в котором использовано охлаждение газа при его адиабатическом расширении.

Лабораторный стенд состоит из насоса и баллона, наполненного воздухом и соединенного с манометром (рис. 1).

Посредством крана баллон может сообщаться с атмосферой. В начале эксперимента давление воздуха в баллоне равно атмосферному, а его температура Т_ОКР равна температуре окружающей среды.

74

Идея метода состоит в том, что находящийся в сосуде газ заставляют совершать изопроцессы, в том числе и адиабатный; измеряя давление в начале и конце каждого процесса по отношению давлений определяют показатель адиабаты. При этом из всего газа, заполняющего сосуд, мысленно выделяют небольшую часть газа массой m, занимающую объём V. Предполагается, что все процессы (сжатие, нагревание или охлаждение) происходят именно с этой частью газа.

Открыв кран, с помощью насоса можно подкачать в баллон некоторое количество воздуха, в результате чего давление в баллоне повысится до некоторого значения p₁. После подкачки следует подождать примерно минуту: за это время в результате теплообмена через стенки температура воздуха внутри баллона опять сравняется  с температурой наружного воздуха. Рассматриваемая нами порция газа массой m займёт объём V₁, то есть будет сжата остальной частью воздуха. Этому состоянию данной части газа соответствует точка 1 на рис. 2.

После того как давление газа в баллоне установилось, быстро выпускаем часть газа из сосуда, после чего сосуд закрываем. Давление в сосуде (и в выделенной порции газа) упадёт до р₂.